
【题目】已知函数f(x)=lnx﹣ax+a,a∈R.
(1)求f(x)的单调区间;
(2)当x≥1时,恒有g(x)=(x+1)f(x)﹣lnx≤0恒成立,求a的取值范围.
【答案】(1)当a≤0时,函数的单调增区间为![]() ,无单调减区间;当a>0时,函数的单调增区间为
,无单调减区间;当a>0时,函数的单调增区间为![]() ,函数的单调减区间为
,函数的单调减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)求导,对参数进行分类讨论,求出对应情况下的单调区间即可;
(2)求出![]() 的导函数,进行二次求导,通过讨论导数的正负,判断函数
的导函数,进行二次求导,通过讨论导数的正负,判断函数![]() 的单调性,结合题意即可进行求解.
的单调性,结合题意即可进行求解.
(1)函数的定义域(0,+∞),![]() ,
,
(i)当![]() 时,
时,![]() 恒成立,f(x)在(0,+∞)上单调递增;
恒成立,f(x)在(0,+∞)上单调递增;
(ii)当a>0时,由![]() 可得,
可得,![]() ,此时函数单调递增,
,此时函数单调递增,
由![]() 可得,x
可得,x![]() ,此时函数单调递减.
,此时函数单调递减.
故当a≤0时,函数的单调增区间为![]() ,无单调减区间;
,无单调减区间;
当a>0时,函数的单调增区间为![]() ,函数的单调减区间为
,函数的单调减区间为![]() .
.
(2)当x≥1时,g(x)=(x+1)(lnx﹣ax+a)﹣lnx=xlnx﹣ax2+a,
![]() =lnx+1﹣2ax,
=lnx+1﹣2ax,
令h(x)=lnx+1﹣2ax,
则![]() .
.
(i)当a≤0时,![]() >0恒成立,h(x)在[1,+∞)上单调递增.
>0恒成立,h(x)在[1,+∞)上单调递增.
h(x)≥h(1)=1﹣2a>0,
即![]() 0,故g(x)在[1,+∞)上单调递增,g(x)≥g(1)=0,不合题意;
0,故g(x)在[1,+∞)上单调递增,g(x)≥g(1)=0,不合题意;
(ii)当0<a![]() 时,h(x)在[1,
时,h(x)在[1,![]() ]上单调递增,
]上单调递增,
![]() =1﹣2a>0,此时g(x)在[1,
=1﹣2a>0,此时g(x)在[1,![]() ]上单调递增,
]上单调递增,
所以g(![]() )>g(1)=0,不合题意;
)>g(1)=0,不合题意;
(iii)当a![]() 时,
时,![]() ,h(x)在[1,+∞)上单调递减,
,h(x)在[1,+∞)上单调递减,
所以![]() ,故
,故![]() ≤0,
≤0,
所以g(x)在[1,+∞)上单调递减,
所以g(x)≤g(1)=0,所以g(x)≤0恒成立.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在传染病学中,通常把从致病刺激物侵入机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表. 请将列联表补充完整,并根据列联表判断是否有![]() 的把握认为潜伏期与患者年龄有关;
的把握认为潜伏期与患者年龄有关;
潜伏期 | 潜伏期 | 总计 | |
50岁以上(含50岁) |
| ||
50岁以下 | 55 | ||
总计 | 200 |
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立. 为了深入研究,该研究团队随机调查了![]() 名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
| |
|
|
|
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.
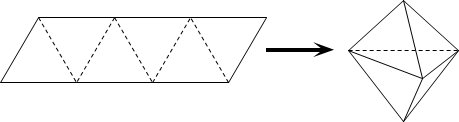
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一工厂计划生产某种当地政府控制产量的特殊产品,月固定成本为1万元,设此工厂一个月内生产该特殊产品![]() 万件并全部销售完.根据当地政府要求产量
万件并全部销售完.根据当地政府要求产量![]() 满足
满足![]() ,每生产
,每生产![]() 件需要再投入
件需要再投入![]() 万元,每1万件的销售收入为
万元,每1万件的销售收入为![]() (万元),且每生产1万件产品政府给予补助
(万元),且每生产1万件产品政府给予补助![]() (万元).(注:月利润=月销售收入+月政府补助-月总成本).
(万元).(注:月利润=月销售收入+月政府补助-月总成本).
(1)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(2)求该工厂在生产这种特殊产品中所获得的月利润最大值(万元)及此时的月生产量(万件)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有![]() 名学生,其中男生
名学生,其中男生![]() 人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了
人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了![]() 名学生进行调查,月消费金额分布在
名学生进行调查,月消费金额分布在![]() 之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
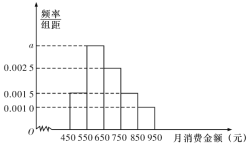
将月消费金额不低于![]() 元的学生称为“高消费群”.
元的学生称为“高消费群”.
(1)求![]() 的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从月消费金额落在![]() ,
,![]() 内的两组学生中抽取
内的两组学生中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,记被抽取的
人,记被抽取的![]() 名学生中属于“高消费群”的学生人数为随机变量
名学生中属于“高消费群”的学生人数为随机变量![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
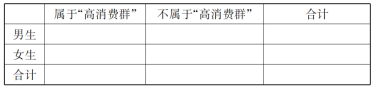
(3)若样本中属于“高消费群”的女生有![]() 人,完成下列
人,完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该校学生属于“高消费群”与“性别”有关?
的把握认为该校学生属于“高消费群”与“性别”有关?
(参考公式: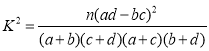 ,其中
,其中![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,
中,![]() 底面ABC,
底面ABC,![]() ,E,F分别为棱PB,PC的中点,过E,F的平面分别与棱AB,AC相交于点D,G,给出以下四个结论:
,E,F分别为棱PB,PC的中点,过E,F的平面分别与棱AB,AC相交于点D,G,给出以下四个结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则以上正确结论的个数是
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东省的生产总值已经连续30年位居全国第一位,如表是广东省从2012年至2018年7年的生产总值以人民币(单位:万亿元)计算的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
广东省生产总值y(单位:万亿元) | 5.71 | 6.25 | 6.78 | 7.28 | 8.09 | 8.97 | 9.73 |
(1)从表中数据可认为x和y的线性相关性较强,求出以x为解释变量、y为预报变量的线性回归方程(系数精确到0.01);
(2)广东省2018年人口约为1.13亿,德国2018年人口约为0.83亿.从人口数量比较看,广东省比德国人口多,但德国2018年的生产总值为4.00万亿美元,以(1)的结论为依据,预测广东省在哪年的生产总值能超过德国在2018年的生产总值?
参考数据:![]() yi=52.81,
yi=52.81,![]() xiyi=230.05,
xiyi=230.05,![]() yi2=411.2153,
yi2=411.2153,![]() xi2=140.
xi2=140.
货币兑换:1美元≈7.03元人民币
参考公式:回归方程![]() x
x![]() 中斜率
中斜率![]() 和截距
和截距![]() 的最小二乘估计公式分别为:
的最小二乘估计公式分别为: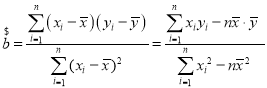 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com