
设某地区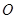 型血的人数占总人口数的比为
型血的人数占总人口数的比为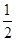 ,现从中随机抽取3人.
,现从中随机抽取3人.
(1)求3人中恰有2人为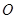 型血的概率;
型血的概率;
(2)记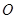 型血的人数为
型血的人数为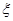 ,求
,求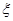 的概率分布与数学期望.
的概率分布与数学期望.
科目:高中数学 来源: 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次任意抽取3道题,独立作答,然后由乙回答剩余3题,每人答对其中的2题就停止答题,即闯关成功。已知6道备选题中,甲能答对其中的4道题,乙答对每道题的概率都是 .
.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.(1)求甲、乙两人考试均合格的概率;(2)求甲答对试题数 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区为了解高二学生作业量和玩电脑游戏的情况,对该地区内所有高二学生采用随机抽样的方法,得到一个容量为200的样本.统计数据如下:
(1)已知该地区共有高二学生42500名,根据该样本估计总体,其中喜欢电脑游戏并认为作业不多的人有多少名?
(2)在A,B,C,D,E,F六名学生中,仅有A,B两名学生认为作业多.如果从这六名学生中随机抽取两名,求至少有一名学生认为作业多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中装有大小形状完全相同的红色球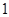 个、黄色球
个、黄色球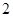 个、蓝色球
个、蓝色球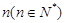 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得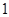 分、摸到黄球得
分、摸到黄球得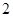 分、摸到蓝球得
分、摸到蓝球得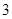 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出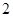 个球,恰有一个是黄色球的概率是
个球,恰有一个是黄色球的概率是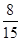 .
.
⑴求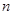 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出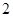 个球,设
个球,设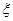 表示所摸
表示所摸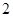 球的得分之和,求
球的得分之和,求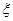 的分布列和数学期望
的分布列和数学期望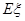 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有编号分别为1,2,3,4,5,6,7, 8,9的九道不同的数学题。某同学从这九道题中一次随机抽取两道题,每题被抽到的概率是相等的,用符号 表示事件“抽到两 题的编号分别为
表示事件“抽到两 题的编号分别为 ,且
,且 <
< ”.
”.
(1)共有多少个基本事件?并列举出来;
(2)求该同学所抽取的两道题的编号之和小于17但不小于11的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种玫瑰花,进货商当天以每支1元从鲜花批发商店购进,以每支2元售出.若当天卖不完,剩余的玫瑰花批发商店以每支0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:支)的频率分布直方图(如图所示),将频率视为概率.(12分)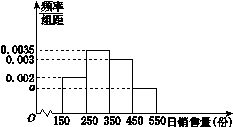
(1)求频率分布直方图中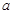 的值;
的值;
(2)若进货量为 (单位支),当n≥X时,求利润Y的表达式;
(单位支),当n≥X时,求利润Y的表达式;
(3)若当天进货量n=400,求利润Y的分布列和数学期望E(Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上
的产量均具有随机性,且互不影响,其具体情况如下表:

(1)设 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求 的分布列;
的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com