
【题目】已知函数f(x)=lnx![]() ,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
,其中a>0.曲线y=f(x)在点(1,f(1))处的切线与直线y=x+1垂直.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在区间[1,e]上的极值和最值.
【答案】(1)f(x)的单调减区间为(0,2),增区间为[2,+∞);(2)f(x)的极小值为f(2)=ln2,无极大值;最小值ln2,最大值1.
【解析】
(1)先求导,由曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直可得
垂直可得![]() ,即可解得
,即可解得![]() ,再分别令
,再分别令![]() 和
和![]() ,即可求解;
,即可求解;
(2)由(1)可知f(x)的极小值为f(2),无极大值,再将极值与端点值比较求得最值即可.
(1)由题,![]() (x>0),
(x>0),
因为曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,
所以![]() ,解得a=2,
,解得a=2,
所以![]() ,
,
令![]() 得0<x<2,令
得0<x<2,令![]() 得x>2,
得x>2,
所以f(x)的单调减区间为(0,2),增区间为[2,+∞)
(2)由(1)可得f(x)在(1,2)上递减,在(2,e)上递增,
故f(x)的极小值为f(2)=ln2,无极大值;
又因为f(1)=1,f(e)![]() ,f(2)=ln2,
,f(2)=ln2,
所以f(x)的最小值为ln2,最大值为1.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】一次循环赛中有2n+1支参赛队,其中每队与其他队均只进行一场比赛,且比赛结果中没有平局。若三支参赛队A、B、C满足:A击败B,B击败C,C击败A,则称它们形成一个“环形三元组”。求:
(1)环形三元组的最小可能数目;
(2)环形三元组的最大可能数目。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左
的左![]() 、
、![]() 右焦点分别为,点
右焦点分别为,点![]() 在椭圆上,且满足
在椭圆上,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设倾斜角为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,求
,求![]() 取最大值时直线
取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.

(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的提高,越来越多的人愿意花更高的价格购买手机.某机构为了解市民使用手机的价格情况,随机选取了100人进行调查,并将这100人使用的手机价格按照![]() ,
,![]() ,…,
,…,![]() 分成6组,制成如图所示的频率分布直方图:
分成6组,制成如图所示的频率分布直方图:
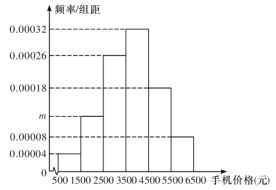
(1)求图中![]() 的值;
的值;
(2)求这组数据的平均数和中位数(同一组中的数据用该组区间的中间值作代表);
(3)利用分层抽样从手机价格在![]() 和
和![]() 的人中抽取5人,并从这5人中抽取2人进行访谈,求抽取出的2人的手机价格在不同区间的概率.
的人中抽取5人,并从这5人中抽取2人进行访谈,求抽取出的2人的手机价格在不同区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com