练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某三棱锥的三视图如图所示，则该三棱锥最长的棱的棱长为（ ）

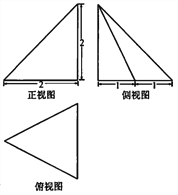
    A. 2 B. C. D. 3

    【答案】D

    【解析】由三视图可得几何体的直观图如图所示：

    有： 面ABC， △ABC中， ， 边上的高为2，

    所以.

    该三棱锥最长的棱的棱长为.

    故选D.

    点睛; 思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2017年10月份郑州市进行了高三学生的体育学业水平测试，为了考察高中学生的身体素质比情况，现抽取了某校1000名（男生800名，女生200名）学生的测试成绩，根据性别按分层抽样的方法抽取100名进行分析，得到如下统计图表：

    男生测试情况：

    抽样情况

    病残免试

    不合格

    合格

    良好

    优秀

    人数

    5

    10

    15

    47

    女生测试情况

    抽样情况

    病残免试

    不合格

    合格

    良好

    优秀

    人数

    2

    3

    10

    2

    （1）现从抽取的1000名且测试等级为“优秀”的学生中随机选出两名学生，求选出的这两名学生恰好是一男一女的概率；

    （2）若测试等级为“良好”或“优秀”的学生为“体育达人”，其它等级的学生（含病残免试）为“非体育达人”，根据以上统计数据填写下面列联表，并回答能否在犯错误的概率不超过0.010的前提下认为“是否为体育达人”与性别有关？

    男性

    女性

    总计

    体育达人

    非体育达人

    总计

    临界值表：

    0.10

    0.05

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    附：（ ，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    (1)若在时取到极值,求的值及的图象在处的切线方程;

    (2)若在时恒成立,求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的离心率为，且以两焦点为直径的圆的内接正方形面积为2．

    （1）求椭圆的标准方程；

    （2）若直线： 与椭圆相交于， 两点，在轴上是否存在点，使直线与的斜率之和为定值？若存在，求出点坐标及该定值，若不存在，试说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某三棱锥的三视图如图所示，则该三棱锥最长的棱的棱长为（ ）

    A. 3 B. C. D. 2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，动点到点的距离和它到直线的距离相等，记点的轨迹为.

    （Ⅰ）求得方程；

    （Ⅱ）设点在曲线上， 轴上一点（在点右侧）满足.平行于的直线与曲线相切于点，试判断直线是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1=3，且an+1﹣3an=3n，（n∈N*），数列{bn}满足bn=3﹣nan．

    （1）求证：数列{bn}是等差数列；

    （2）设，求满足不等式的所有正整数n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，三棱柱中，已知侧面.

    （1）求证： 平面；

    （2）是棱长上的一点，若二面角的正弦值为，求的长.

    查看答案和解析>>

    同步练习册答案