
【题目】已知a,b分别是△ABC内角A,B的对边,且bsin2A=![]() acos Asin B,函数f(x)=sin Acos2x-sin2
acos Asin B,函数f(x)=sin Acos2x-sin2![]() sin 2x,x∈
sin 2x,x∈![]() .
.
(1)求A;
(2)求函数f(x)的值域.
【答案】(1) ![]() ;(2)
;(2) 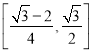 .
.
【解析】试题分析:
(1)由已知结合正弦定理,求出![]() 的值,从而求出
的值,从而求出![]() 的值;
的值;
(2)由![]() 化简函数
化简函数![]() 为正弦型函数,求出
为正弦型函数,求出![]() 时
时![]() 的值域即可.
的值域即可.
试题解析:
(1)在△ABC中,bsin2A=![]() acos Asin B,
acos Asin B,
由正弦定理得,sin Bsin2A=![]() sin Acos Asin B,
sin Acos Asin B,
又A,B为△ABC的内角,故sin Asin B≠0,
∴tan A=![]() =
=![]() ,
,
又A∈(0,π),∴A=![]() .
.
(2)由A=![]() ,
,
∴函数f(x)=sin Acos2x-sin2![]() sin 2x
sin 2x
=![]() cos2x-
cos2x-![]() sin 2x
sin 2x
=![]() ·
·![]() -
-![]() ·
·![]() sin 2x
sin 2x
=-![]()
![]() +
+![]()
=-![]() sin
sin![]() +
+![]() ,
,
∵x∈![]() ,∴-
,∴-![]() ≤2x-
≤2x-![]() ≤
≤![]() ,
,
∴-![]() ≤sin
≤sin![]() ≤1,
≤1,
∴![]() ≤-
≤-![]() sin
sin![]() +
+![]() ≤
≤![]() ,
,
所以f(x)的值域为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,C1的参数方程为 (t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(Ⅰ)说明C2是哪种曲线,并将C2的方程化为普通方程;
(Ⅱ)C1与C2有两个公共点A,B,定点P的极坐标![]() ,求线段AB的长及定点P到A,B两点的距离之积.
,求线段AB的长及定点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张A4纸的长宽之比为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.现分别将△
的中点.现分别将△![]() ,△
,△![]() 沿
沿![]() ,
, ![]() 折起,且
折起,且![]() ,
, ![]() 在平面
在平面![]() 同侧,下列命题正确的是__________.(写出所有正确命题的序号)
同侧,下列命题正确的是__________.(写出所有正确命题的序号)

①![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点共面;
四点共面;
②当平面![]() 平面
平面![]() 时,
时, ![]() 平面
平面![]() ;
;
③当![]() ,
, ![]() 重合于点
重合于点![]() 时,平面
时,平面![]() 平面
平面![]() ;
;
④当![]() ,
, ![]() 重合于点
重合于点![]() 时,设平面
时,设平面![]() 平面
平面![]()
![]() ,则
,则![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=2,数列{anan+1}是公比为q (q>0)的等比数列,则数列{an}的前2n项和S2n=____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
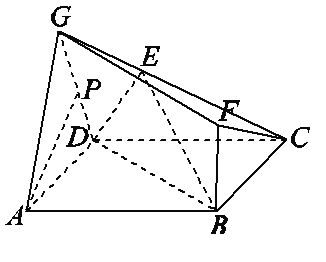
【题目】如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,BF⊥平面ABCD,∠GDC=90°,点E是线段GC上除两端点外的一点,若点P为线段GD的中点.
(Ⅰ)求证:AP⊥平面GCD;
(Ⅱ)求证:平面ADG∥平面FBC;
(Ⅲ)若AP∥平面BDE,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点
经过点 ,离心率为
,离心率为![]() .
.
(1)求椭圆E的标准方程;
(2)若A1,A2分别是椭圆E的左、右顶点,过点A2作直线l与x轴垂直,点P是椭圆E上的任意一点(不同于椭圆E的四个顶点),连接PA1交直线l于点B,点Q为线段A2B的中点,求证:直线PQ与椭圆E只有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),长轴长为4,离心率为
(a>b>0),长轴长为4,离心率为![]() .
.
(Ⅰ)椭圆的求椭圆的标准方程;
(Ⅱ)设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com