
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(I)根据![]()
![]() ,设直线方程为
,设直线方程为![]() ,
,![]()
确定![]() 的坐标,由
的坐标,由![]() 确定得到
确定得到![]() ,
,
再根据![]() 点在椭圆上,求得
点在椭圆上,求得![]() 进一步即得所求
进一步即得所求![]() ;
;
(2)由![]() 可设
可设![]() ,
,
得到椭圆的方程为![]() ,
,
由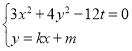 得
得![]()
根据动直线![]() 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
得到![]() ,整理得
,整理得![]() .
.
确定![]() 的坐标
的坐标![]() ,
,
又![]() ,
, ![]()
![]()
若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,那么
,那么![]()
可得![]() ,由
,由![]() 恒成立,故
恒成立,故![]() ,得解.
,得解.
试题解析:(1)∵![]()
![]() ,设直线方程为
,设直线方程为![]() ,
,![]()
令![]() ,则
,则![]() ,∴
,∴![]() , 2分
, 2分
∴![]() 3分
3分
∵![]() ,∴
,∴![]() =
=![]() ,
,
整理得![]() 4分
4分
∵![]() 点在椭圆上,∴
点在椭圆上,∴![]() ,∴
,∴![]() 5分
5分
∴![]() 即
即![]() ,∴
,∴![]() 6分
6分
(2)∵![]() 可设
可设![]() ,
,
∴椭圆的方程为![]() 7分
7分
由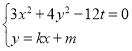 得
得![]() 8分
8分
∵动直线![]() 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
∴![]() ,即
,即![]()
整理得![]() 9分
9分
设![]()
![]() 则有
则有![]() ,
,![]()
∴![]() 10分
10分
又![]() ,
,![]()
![]()
若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,
,
∴![]() 恒成立
恒成立
整理得![]() , 12分
, 12分
∴![]() 恒成立,故
恒成立,故![]()
所求椭圆方程为![]() 13分
13分


科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.
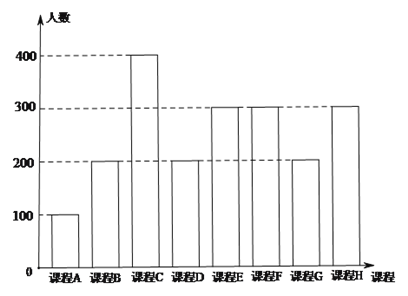
图中,课程![]() 为人文类课程,课程
为人文类课程,课程![]() 为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组
为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组![]() ”).
”).
(Ⅰ)在“组![]() ”中,选择人文类课程和自然科学类课程的人数各有多少?
”中,选择人文类课程和自然科学类课程的人数各有多少?
(Ⅱ)某地举办自然科学营活动,学校要求:参加活动的学生只能是“组![]() ”中选择
”中选择![]() 课
课
程或![]() 课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择
课程的同学,并且这些同学以自愿报名缴费的方式参加活动. 选择![]() 课程的学生中有
课程的学生中有![]() 人参加科学营活动,每人需缴纳
人参加科学营活动,每人需缴纳![]() 元,选择
元,选择![]() 课程的学生中有
课程的学生中有![]() 人参加该活动,每人需缴纳
人参加该活动,每人需缴纳![]() 元.记选择
元.记选择![]() 课程和
课程和![]() 课程的学生自愿报名人数的情况为
课程的学生自愿报名人数的情况为![]() ,参加活动的学生缴纳费用总和为
,参加活动的学生缴纳费用总和为![]() 元.
元.
①当![]() 时,写出
时,写出![]() 的所有可能取值;
的所有可能取值;
②若选择![]() 课程的同学都参加科学营活动,求
课程的同学都参加科学营活动,求![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
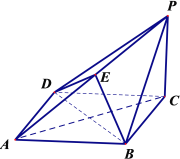
【题目】如图,在四棱锥![]() 中, 底面
中, 底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的体积的
的体积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆
为椭圆![]() 的左焦点,且
的左焦点,且![]() 是边长为2的等边三角形.
是边长为2的等边三角形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据如图给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是( ) 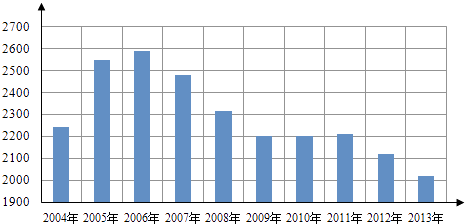
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校举行的 “青年歌手大选赛”吸引了众多有才华的学生参赛.为了了解本次比赛成绩情况,从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
组别 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0.16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0.40 |
第4组 | [80,90) | ▓ | 0.08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |
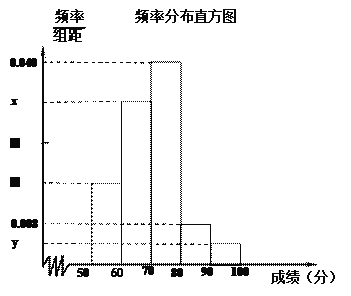
(1)求出![]() 的值;
的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取2名同学参加元旦晚会,求所抽取的2名同学中至少有1名同学来自第5组的概率;
(3)根据频率分布直方图,估计这50名学生成绩的众数、中位数和平均数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com