
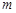 是给定的正整数,有序数组(
是给定的正整数,有序数组(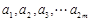 )中
)中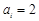 或
或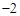
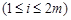 .
.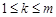 ,
,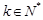 ,都有
,都有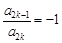 ”的有序数组(
”的有序数组(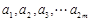 )的个数
)的个数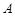 ;
;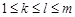 ,
,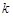 ,
,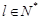 ,都有
,都有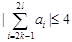 成立,求满足“存在
成立,求满足“存在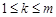 ,使得
,使得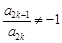 ”的有序数组(
”的有序数组(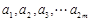 )的个数
)的个数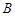 .
. ,(2)
,(2) .
.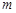 组,每组有2种可能,各组可能互不影响,共有
组,每组有2种可能,各组可能互不影响,共有 种可能,
种可能,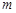 个.另外条件“对任意的
个.另外条件“对任意的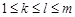 ,
,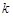 ,
,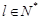 ,都有
,都有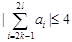 成立”控制不能出现各组都为2或-2的情况,而是间隔出现(2,2)、(-2,-2).
成立”控制不能出现各组都为2或-2的情况,而是间隔出现(2,2)、(-2,-2). ,都有
,都有 ,则
,则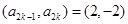 或
或
 种,所以
种,所以 共有
共有 种不同的选择,所以
种不同的选择,所以 . 5分
. 5分 时,那么这一组有
时,那么这一组有 种,其余的由(1)知有
种,其余的由(1)知有 ,所有共有
,所有共有 ;
; 时,因为条件对任意的
时,因为条件对任意的 ,都有
,都有 成立得这两组共有
成立得这两组共有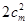 ,
, ,所有共有
,所有共有 ;
; . 10分
. 10分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com