
【题目】已知函数![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() ,
,![]() 时,证明:
时,证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,分类讨论:(1)
,分类讨论:(1)![]() ;(2)
;(2)![]() ,可得单调区间;(2)当
,可得单调区间;(2)当![]() 时,要 证
时,要 证
![]() 转化为证
转化为证![]() ,设
,设![]() ,判断其单调性,得
,判断其单调性,得![]() ,此题得证。
,此题得证。
(1)当![]() 时,
时, ![]()
![]()
![]()
讨论:1’当![]() 时,
时, ![]() ,
, ![]() ,
, ![]()
![]()
此时函数![]() 的单调递减区间为
的单调递减区间为![]() ,无单调递增区间
,无单调递增区间
2’当![]() 时,令
时,令![]()
![]() 或
或![]()
①当![]() ,即
,即![]() 时,此时
时,此时![]()
![]()
此时函数![]() 单调递增区间为
单调递增区间为![]() ,无单调递减区间
,无单调递减区间
②当![]() ,即
,即![]() 时,此时在
时,此时在![]() 和
和![]() 上函数
上函数![]() ,
,
在![]() 上函数
上函数![]() ,此时函数
,此时函数![]() 单调递增区间为
单调递增区间为![]() 和
和![]() ;
;
单调递减区间为![]()
③当![]() ,即
,即![]() 时,此时函数
时,此时函数![]() 单调递增区间为
单调递增区间为![]() 和
和![]() ;
;
单调递减区间为![]()
(2)证明:当![]() 时
时 ![]()
只需证明: ![]() 设
设![]()
![]()
问题转化为证明![]() ,
, ![]()
令![]() ,
, ![]() ,
,
![]() 为
为![]() 上的增函数,且
上的增函数,且![]() ,
, ![]()
![]() 存在唯一的
存在唯一的![]() ,使得
,使得![]() ,
, ![]()
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]()
![]()
![]()
![]() 不等式得证
不等式得证


科目:高中数学 来源: 题型:
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照5%的比例进行分层抽样,统计结果按
内)中,按照5%的比例进行分层抽样,统计结果按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,整理如下图:
分组,整理如下图:
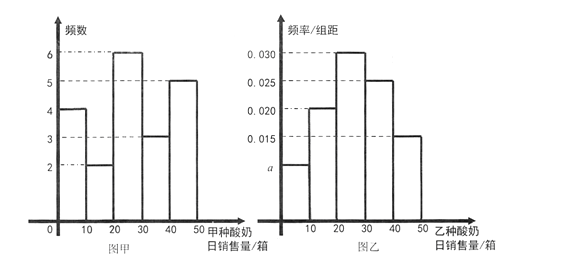
(Ⅰ)写出频率分布直方图(图乙)中![]() 的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为
的值;记所抽取样本中甲种酸奶与乙种酸奶日销售量的方差分别为![]() ,
, ![]() ,试比较
,试比较![]() 与
与![]() 的大小(只需写出结论);
的大小(只需写出结论);
(Ⅱ)从甲种酸奶日销售量在区间![]() 的数据样本中抽取3个,记在
的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)估计1200个日销售量数据中,数据在区间![]() 中的个数.
中的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年五一假期期间,高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
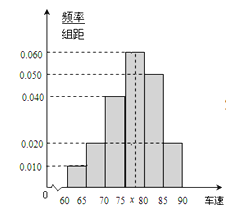
(Ⅰ)求这40辆小型车辆车速的众数和中位数以及平均数的估计值.
(Ⅱ)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校组织“中国诗词”竞赛,在“风险答题”的环节中,共为选手准备了![]() 三类不同的题目,选手每答对一个
三类不同的题目,选手每答对一个![]() 类、
类、![]() 类或
类或![]() 类的题目,将分别得到
类的题目,将分别得到![]() 分,
分, ![]() 分,
分, ![]() 分,但如果答错,则相应要扣去
分,但如果答错,则相应要扣去![]() 分,
分, ![]() 分,
分, ![]() 分,根据平时训练经验,选手甲答对
分,根据平时训练经验,选手甲答对![]() 类、
类、![]() 类或
类或![]() 类的题目的概率分别为
类的题目的概率分别为![]() 、
、![]() 、
、![]() ,若要每一次答题的均分更大一些,则选手甲应选择的题目类型应为_________.(填
,若要每一次答题的均分更大一些,则选手甲应选择的题目类型应为_________.(填![]() ,
, ![]() 或
或![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区的物业部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,并画出程序框图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com