
分析 (1)直接运用零点分段法求解含绝对值不等式;
(2)先求出$\frac{1}{m}$+$\frac{2}{n}$的最小值为8,再用绝对值三角不等式将问题等价为:|a+2|≤8,解出即可.
解答 解:(1)不等式:f(x)<4-|x-1|可写成,
|3x+2|+|x-1|<4,用“零点分段法”解答如下:
①当x≥1时,3x+2+x-1<4,x∈∅;
②当-$\frac{2}{3}$≤x<1时,3x+2-x+1<4,解得,-$\frac{2}{3}$≤x<$\frac{1}{2}$;
③当x<-$\frac{2}{3}$时,-3x-2-1+x<4,解得,-$\frac{5}{4}$<x<-$\frac{2}{3}$,
综合以上讨论得,不等式的解集为:{x|-$\frac{5}{4}$<x<$\frac{1}{2}$};
(2)因为2m+1=1,且m>0,n>0,
所以,$\frac{1}{m}$+$\frac{2}{n}$=($\frac{1}{m}$+$\frac{2}{n}$)(2m+n)=2+2+$\frac{n}{m}$+$\frac{4m}{n}$≥8,
即$\frac{1}{m}$+$\frac{2}{n}$的最小值为8,
根据题意问题等价为:|3x-a|-f(x)≤8恒成立,
即|3x-a|-|3x+2|≤8对任意实数x恒成立,
再由绝对值三角不等式得,
|3x-a|-|3x+2|≤|a+2|≤8,
解得,a∈(0,6],
所以,实数a的取值范围为:(0,6].
点评 本题主要考查了绝对值不等式的解法,以及绝对值三角不等式的应用和不等式恒成立问题的解法,考查了分类讨论与等价转化思想,属于中档题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | 不过点P且与l垂直的直线 | B. | 不过点P且与l平行的直线 | ||
| C. | 过点P且与l垂直的直线 | D. | 过点P且与l平行的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
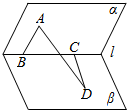 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-∞,-1)∪(3,+∞) | C. | [-3,1] | D. | (-∞,-1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 1 | C. | 16或1 | D. | $\frac{16}{3}$或3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3} | B. | {1,2,3} | C. | {1,2,3,4} | D. | {1,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com