
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,坐标原点为
,坐标原点为![]() .椭圆
.椭圆![]() 的动弦
的动弦![]() 过右焦点
过右焦点![]() 且不垂直于坐标轴,
且不垂直于坐标轴, ![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]()
(I)证明:点![]() 在直线
在直线![]() 上;
上;
(Ⅱ)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的面积.
的面积.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
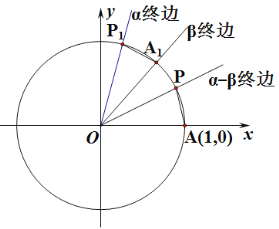
【题目】必修四第一章我们借助圆的对称性学习了诱导公式,如![]() 在直观上讲单位圆中,当两个角的终边关于
在直观上讲单位圆中,当两个角的终边关于![]() 轴对称时,这两个角的正弦值相等;再如
轴对称时,这两个角的正弦值相等;再如![]() 在单位圆中,当两个角的终边关于原点中心对称时,这两个角的正弦值互为相反数.观察这些诱导公式,可以发现它们都是特殊角与任意角
在单位圆中,当两个角的终边关于原点中心对称时,这两个角的正弦值互为相反数.观察这些诱导公式,可以发现它们都是特殊角与任意角![]() 的三角函数的恒等关系.我们如果将特殊角换为任意角
的三角函数的恒等关系.我们如果将特殊角换为任意角![]() ,那么任意角
,那么任意角![]() 与
与![]() 的和(或差)的三角函数与
的和(或差)的三角函数与![]() ,
,![]() 的三角函数会有什么关系呢?如果已知
的三角函数会有什么关系呢?如果已知![]() ,
,![]() 的正弦余弦,能由此推出
的正弦余弦,能由此推出![]() 的正弦余弦吗?下面是某高一学生在老师的指导下自行探究
的正弦余弦吗?下面是某高一学生在老师的指导下自行探究![]() 与角
与角![]()
![]() 的正弦余弦之间的关系的部分过程,请你顺着这位同学的思路以及老师的提示将探究过程完善,并完成后面的题目.探究过程如下:
的正弦余弦之间的关系的部分过程,请你顺着这位同学的思路以及老师的提示将探究过程完善,并完成后面的题目.探究过程如下:
不妨令![]() 如图,设单位圆与
如图,设单位圆与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() 以
以![]() 轴的非负半轴为始边作角
轴的非负半轴为始边作角![]() 它们的终边分别与单位圆相交于点
它们的终边分别与单位圆相交于点![]() 连接
连接![]() 若把扇形
若把扇形![]() 绕着点
绕着点![]() 旋转
旋转![]() 角,则点
角,则点![]() 分别与点
分别与点![]() 重合. ……(未完待续)
重合. ……(未完待续)
(提示一:任意一个圆绕着其圆心旋转任意角后都与原来的圆重合,这一性质叫做圆的旋转对称性)(提示二:平面上任意两点![]() 间的距离公式
间的距离公式![]() )
)
(1)完善上述探究过程;
(2)利用(1)中的结论解决问题:已知![]()
![]() 是第三象限角,求
是第三象限角,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某盒子内装有三种颜色的玻璃球,一位同学每次从中随机拿出一个玻璃球,观察颜色后再放回,重复了50次,得到的信息如下:观察到红色26次、蓝色13次.如果从这个盒子内任意取一个玻璃球,估计:
(1)这个球既不是红色也不是蓝色的概率;
(2)这个球是红色或者是蓝色的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)抛物线的开口向 、对称轴为直线 、顶点坐标 ;
(2)当![]() 时,函数有最 值,是 ;
时,函数有最 值,是 ;
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
(4)该函数图象可由![]() 的图象经过怎样的平移得到的?
的图象经过怎样的平移得到的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() ,
,![]() 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,![]()
假设所有病人的康复时间互相独立,从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的
组选出的
人记为乙.
(Ⅰ)求甲的康复时间不少于14天的概率;
(Ⅱ)如果![]() ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ)当![]() 为何值时,
为何值时,![]() ,
,![]() 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“五四青年节”到来之际,启东中学将开展一系列的读书教育活动.为了解高二学生读书教育情况,决定采用分层抽样的方法从高二年级![]() 四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
四个社团中随机抽取12名学生参加问卷调査.已知各社团人数统计如下:
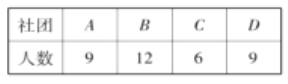
(1)若从参加问卷调查的12名学生中随机抽取2名,求这2名学生来自同一个社团的概率;
(2)在参加问卷调查的12名学生中,从来自![]() 三个社团的学生中随机抽取3名,用
三个社团的学生中随机抽取3名,用![]() 表示从
表示从![]() 社团抽得学生的人数,求
社团抽得学生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点.
上一点.
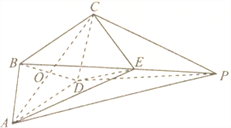
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com