【题目】新高考方案规定，普通高中学业水平考试分为合格性考试（合格考）和选择性考试（选择考）.其中“选择考”成绩将计入高考总成绩，即“选择考”成绩根据学生考试时的原始卷面分数，由高到低进行排序，评定为
、
、
、
、
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍，为了更好地分析该校学生“选择考”的水平情况，统计了该校2016年和2018年“选择考”成绩等级结果，得到如下图表：
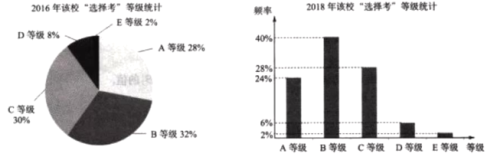
针对该校“选择考”情况，2018年与2016年比较，下列说法正确的是（ ）
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
科目：高中数学 来源： 题型：
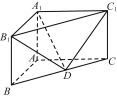
【题目】在直三棱柱ABC-A1B1C1中，已知AB⊥AC，AB＝2，AC＝4，AA1＝3，D是BC的中点．
(1) 求直线DC1与平面A1B1D所成角的正弦值；
(2) 求二面角
的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的首项
，且
，
.
（1）证明：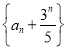
是等比数列；
（2）若
，中是否存在连续三项成等差数列？若存在，写出这三项，若不存在，请说明理由；
（3）若是递减数列，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
有时可用函数
描述学习某学科知识的掌握程度，其中x表示某学科知识的学习次数（
），
表示对该学科知识的掌握程度，正实数a与学科知识有关.
（1） 证明：当
时，掌握程度的增加量
总是下降；
（2） 根据经验，学科甲、乙、丙对应的a的取值区间分别为
,
,
.当学习某学科知识6次时，掌握程度是85%，请确定相应的学科.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知F1、F2分别是双曲线
1（a＞0，b＞0）的左、右焦点，若双曲线的右支上存在一点P，使得（
）
0（O为坐标原点），且|PF1|
|PF2|，则双曲线的离心率的取值范围是_____．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】秉承提升学生核心素养的理念，学校开设以提升学生跨文化素养为核心的多元文化融合课程.选某艺术课程的学生唱歌、跳舞至少会一项，已知会唱歌的有
人，会跳舞的有
人，现从中选人，设
为选出的人中既会唱歌又会跳舞的人数，且
(1)求选该艺术课程的学生人数;
(2)写出的概率分布列并计算
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】第十一届全国少数民族传统体育运动会在河南郑州举行，某项目比赛期间需要安排3名志愿者完成5项工作，每人至少完成一项，每项工作由一人完成，则不同的安排方式共有多少种
A.60B.90C.120D.150
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
