
【题目】如图,正方形ABCD的中心为O , 四边形OBEF为矩形,平面OBEF⊥平面ABCD , 点G为AB的中点,AB=BE=2.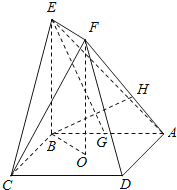
(1)求证:EG∥平面ADF;
(2)求二面角O-EF-C的正弦值;
(3)设H为线段AF上的点,且AH= ![]() HF , 求直线BH和平面CEF所成角的正弦值.
HF , 求直线BH和平面CEF所成角的正弦值.
【答案】
(1)
解:证明:找到 ![]() 中点
中点 ![]() ,连结
,连结 ![]() ,
,
∵矩形 ![]() ,∴
,∴ ![]()
∵ ![]() 、
、 ![]() 是中点,∴
是中点,∴ ![]() 是
是 ![]() 的中位线
的中位线
∴ ![]() 且
且 ![]()
∵ ![]() 是正方形
是正方形 ![]() 中心
中心
∴ ![]()
∴ ![]() 且
且 ![]()
∴四边形 ![]() 是平行四边形
是平行四边形
∴ ![]()
∵ ![]() 面
面 ![]()
∴ ![]() 面
面 ![]()
(2)
解:如图所示建立空间直角坐标系 ![]()
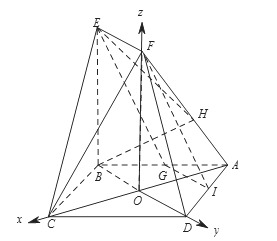
![]() ,
, ![]() ,
, ![]() ,
, ![]()
设面 ![]() 的法向量
的法向量 ![]()
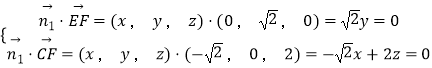
得: 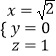
∴ ![]()
∵ ![]() 面
面 ![]() ,
,
∴面 ![]() 的法向量
的法向量 ![]()
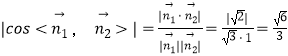
![]()
(3)
∵ ![]()
∴ ![]()
设 ![]()
∴ ![]()
得: 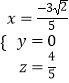
![]()
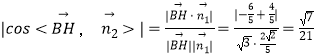
【解析】(1)取AD的中点I,连接FI,证明四边形EFIG是平行四边形,可得EG∥FI,利用线面平行的判定定理证明:EG∥平面ADF;
(2)建立如图所示的坐标系O﹣xyz,求出平面OEF的法向量,平面OEF的法向量,利用向量的夹角公式,即可求二面角O﹣EF﹣C的正弦值;
(3)求出 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),利用向量的夹角公式求出直线BH和平面CEF所成角的正弦值
),利用向量的夹角公式求出直线BH和平面CEF所成角的正弦值
【考点精析】关于本题考查的直线与平面平行的判定和空间角的异面直线所成的角,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则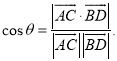 才能得出正确答案.
才能得出正确答案.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图所示的几何体,关于其结构特征,下列说法不正确的是
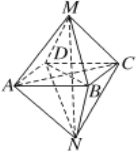
A. 该几何体是由两个同底的四棱锥组成的几何体
B. 该几何体有12条棱、6个顶点
C. 该几何体有8个面,并且各面均为三角形
D. 该几何体有9个面,其中一个面是四边形,其余均为三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
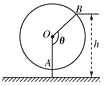
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图. 图中A点表示十月的平均最高气温约为![]() ,B点表示四月的平均最低气温约为
,B点表示四月的平均最低气温约为![]() . 下面叙述不正确的是 ( )
. 下面叙述不正确的是 ( )

A. 各月的平均最低气温都在![]() 以上
以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,并且
的前n项和,并且![]() ,对任意正整数n,
,对任意正整数n, ![]() ;设
;设
![]() .
.
(Ⅰ) 证明:数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(Ⅱ) 设![]() ,求证: 数列
,求证: 数列![]() 不可能为等比数列。
不可能为等比数列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则![]() 的取值范围是( )
的取值范围是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com