
【题目】暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.
(1)写出旅行团每人需交费用![]() (单位:元)与旅行团人数
(单位:元)与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】“双十二”是继“双十一”之后的又一个网购狂欢节,为了刺激“双十二”的消费,某电子商务公司决定对“双十一”的网购者发放电子优惠券.为此,公司从“双十一”的网购消费者中用随机抽样的方法抽取了100人,将其购物金额(单位:万元)按照![]() ,
, ![]() 分组,得到如下频率分布直方图:
分组,得到如下频率分布直方图:
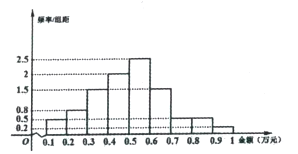
根据调查,该电子商务公司制定了发放电子优惠券的办法如下:

(1)求购物者获得电子优惠券金额的平均数;
(2)从购物者中随机抽取10人,这10人中获得电子优惠券的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数![]() ,若存在区间
,若存在区间![]() ,使得
,使得![]() 同时满足,①
同时满足,①![]() 在
在![]() 上是单调函数,②当
上是单调函数,②当![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域也为
的值域也为![]() ,则称区间
,则称区间![]() 为该函数的一个“和谐区间”
为该函数的一个“和谐区间”
(1)求出函数![]() 的所有“和谐区间”
的所有“和谐区间”![]() ;
;
(2)函数![]() 是否存在“和谐区间”
是否存在“和谐区间”![]() ?若存在,求出实数a,b的值;若不存在,请说明理由
?若存在,求出实数a,b的值;若不存在,请说明理由
(3)已知定义在![]() 上的函数
上的函数![]() 有“和谐区间”,求正整数k取最小值时实数m的取值范围.
有“和谐区间”,求正整数k取最小值时实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次社会实践活动中,某数学调研小组根据车间持续5个小时的生产情况画出了某种产品的总产量![]() (单位:千克)与时间
(单位:千克)与时间![]() (单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
(单位:小时)的函数图像,则以下关于该产品生产状况的正确判断是( ).
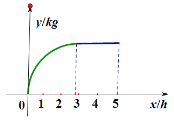
A.在前三小时内,每小时的产量逐步增加
B.在前三小时内,每小时的产量逐步减少
C.最后一小时内的产量与第三小时内的产量相同
D.最后两小时内,该车间没有生产该产品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的方程为
的方程为![]() ,以
,以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,取相同的长度单位建立极坐标系,直线
轴非负半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程和椭圆
的直角坐标方程和椭圆![]() 的参数方程;
的参数方程;
(2)设![]() 为椭圆
为椭圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,曲线C1的参数方程为![]() 以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]()
(1)求曲线C1与C2的直角坐标方程;
(2)当C1与C2有两个公共点时,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表:
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:11 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:50 | 12月20日 | 7:31 |
表2:某年1月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15 | 2月19日 | 7:02 | 2月28日 | 6:49 |
(1)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(2)甲、乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立,记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的 分布列和数学期望;
的 分布列和数学期望;
(3)将表1和表2的升旗时刻化为分数后作为样本数据(如7:31化为![]() ),记表2中所有升旗时刻对应数据的方差为
),记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com