
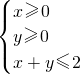 确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是________.
确定的平面区域内,则点N(a+b,a-b)所在平面区域的面积是________.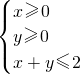 ,可得
,可得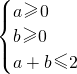
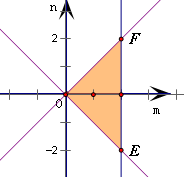
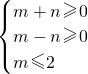
 ×EF×2=4.
×EF×2=4.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 9 |
| PM |
| MQ |
| 4 |
| 17 |
| ON |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| x2 |
| 4 |
| 1 |
| 2 |
| x2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
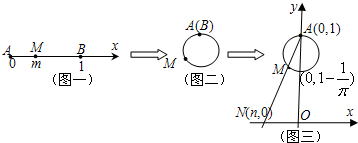 如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )
如图揭示了一个由区间(0,1)到实数集R上的对应过程:区间(0,1)内的任意实数m与数轴上的线段AB(不包括端点)上的点M一一对应(图一),将线段AB围成一个圆,使两端A,B恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1)(图三).图三中直线AM与x轴交于点N(n,0),由此得到一个函数n=f(m),则下列命题中正确的序号是( )| 1 |
| 2 |
| 1 |
| 2 |
| A、(1)(3)(4) |
| B、(1)(2)(3) |
| C、(1)(2)(4) |
| D、(1)(2)(3)(4) |
查看答案和解析>>
科目:高中数学 来源:2008年上海市普陀区高考数学二模试卷(解析版) 题型:解答题
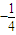 .
.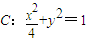 上;
上;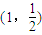 ,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;
,试求△MAB面积的最大值,并求此时直线AB的斜率kAB;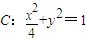 内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.
内一点,过椭圆C中心的直线AB与椭圆分别交于A、B两点.则当且仅当kOM=-kAB时,△MAB的面积取得最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com