
分析 (1)设等差数列{an}的公差为d,运用等差数列的求和公式和通项公式,求得首项和公差,即可得到所求和;
(2)求得$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),运用数列的求和方法:裂项相消求和,化简整理,再由不等式的性质即可得证.
解答 解:(1)设等差数列{an}的公差为d,
S3=$\frac{1}{2}$(a1+a3)×3=3a2=15⇒a2=5,
∴$d=\frac{{{a_4}-{a_2}}}{2}=2$,a1=3,
∴an=3+2(n-1)=2n+1,
${S_n}=\frac{3+2n+1}{2}•n=n(n+2)$;
(2)证明:$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
则${T_n}=\frac{1}{1×3}+\frac{1}{2×4}+…+\frac{1}{n(n+2)}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n}-\frac{1}{n+2})$
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)<$\frac{3}{4}$.
点评 本题考查等差数列的通项公式和求和公式的运用,以及数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| lnx | 0 | 0.69 | 1.10 | 1.39 | 1.61 |
| x-2 | -1 | 0 | 1 | 2 | 3 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 26 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | $2+\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120种 | B. | 96种 | C. | 60种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
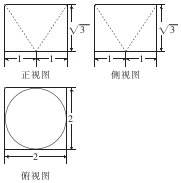
| A. | 8($\sqrt{3}$+1)+π | B. | 8($\sqrt{3}$+1)+2π | C. | 8($\sqrt{3}$+1)一π | D. | 8($\sqrt{3}$+l) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=$\frac{1}{4}$x | B. | y2=-$\frac{1}{4}$x | C. | y2=-4x | D. | x2=-4y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com