
【题目】食品安全一直是人们关心和重视的问题,学校的食品安全更是社会关注的焦点.某中学为了加强食品安全教育,随机询问了36名不同性别的中学生在购买食品时是否看保质期,得到如下“性别”与“是否看保质期”的列联表:
男 | 女 | 总计 | |
看保质期 | 8 | 22 | |
不看保持期 | 4 | 14 | |
总计 |
(1)请将列联表填写完整,并根据所填的列联表判断,能否有![]() 的把握认为“性别”与“是否看保质期”有关?
的把握认为“性别”与“是否看保质期”有关?
(2)从被询问的14名不看保质期的中学生中,随机抽取3名,求抽到女生人数![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,(
,(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】方程ay=b2x2+c中的a,b,c∈{﹣3,﹣2,0,1,2,3},且a,b,c互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )
A.60条
B.62条
C.71条
D.80条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 的线性回归直线方程为
的线性回归直线方程为![]() ,且
,且![]() ,
,![]() 之间的一组相关数据如下表所示,则下列说法错误的为
之间的一组相关数据如下表所示,则下列说法错误的为

A.变量![]() ,
,![]() 之间呈现正相关关系B.可以预测,当
之间呈现正相关关系B.可以预测,当![]() 时,
时,![]()
C.![]() D.由表格数据可知,该回归直线必过点
D.由表格数据可知,该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“节约用水”自古以来就是中华民族的优良传统.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如下图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.

(l)求在未来连续3个月里,有连续2个月的月用水量都不低于12吨且另1个月的月用水量低于4吨的概率;
(2)用![]() 表示在未来3个月里月用水量不低于12吨的月数,求随杌变量
表示在未来3个月里月用水量不低于12吨的月数,求随杌变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,其中
,其中![]() .
.
(1)写出集合![]() 中的所有元素;
中的所有元素;
(2)设![]() ,证明“
,证明“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
(3)设集合![]() ,设
,设![]() ,使得
,使得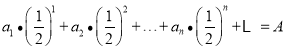 ,且
,且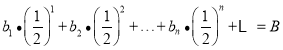 ,试判断“
,试判断“![]() ”是“
”是“![]() ”的什么条件并说明理由.
”的什么条件并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动爱好者对自己的步行运动距离![]() (单位:千米)和步行运动时间
(单位:千米)和步行运动时间![]() (单位:分钟)进行统计,得到如下的统计资料:
(单位:分钟)进行统计,得到如下的统计资料:

如果![]() 与
与![]() 存在线性相关关系,
存在线性相关关系,
(1)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(2)将![]() 分钟的时间数据
分钟的时间数据![]() 称为有效运动数据,现从这6个时间数据
称为有效运动数据,现从这6个时间数据![]() 中任取3个,求抽取的3个数据恰有两个为有效运动数据的概率。
中任取3个,求抽取的3个数据恰有两个为有效运动数据的概率。
参考数据:![]() ,
,
参考公式: ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).

(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com