
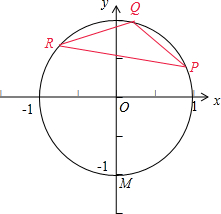
 解:由题意可得,OP2=OQ2=OR2=1,故点P、Q、R都在以原点O为圆心,半径等于1的单位圆上.
解:由题意可得,OP2=OQ2=OR2=1,故点P、Q、R都在以原点O为圆心,半径等于1的单位圆上.

科目:高中数学 来源:浙江省温州中学2011-2012学年高二下学期期末考试数学理科试题 题型:013
若△PQR的三个顶点坐标分别为P(cosA,sinA),Q(cosB,sinB),R(cosC,sinC),其中A,B,C是△ABC的三个内角且满足A<B<C,则△PQR的形状是
A.锐角或直角三角形
B.钝角或直角三角形
C.锐角三角形
D.钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com