
����Ŀ���������������ҹ���������ˮƽ����ߣ����ֳ���ͨ��ҵ�õ�Ѹ�ͷ�չ��ij���������г���2017��ɽ��Ķ��ֳ�����ǰ��ʹ��ʱ�䣨���¼�ơ�ʹ��ʱ�䡱������ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ1��


ͼ1 ͼ2
��1���ǡ���![]() ��ɽ��Ķ��ֳ������ѡȡһ�����ó���ʹ��������
��ɽ��Ķ��ֳ������ѡȡһ�����ó���ʹ��������![]() ��Ϊ�¼�
��Ϊ�¼�![]() ���Թ���
���Թ���![]() �ĸ��ʣ�
�ĸ��ʣ�
��2�����ݸ����������г�����ʷ���ϣ��õ�ɢ��ͼ��ͼ2������![]() (��λ����)��ʾ���ֳ���ʹ��ʱ�䣬
(��λ����)��ʾ���ֳ���ʹ��ʱ�䣬![]() (��λ����Ԫ)��ʾ��Ӧ�Ķ��ֳ���ƽ�����۸���ɢ��ͼ�������ɲ���
(��λ����Ԫ)��ʾ��Ӧ�Ķ��ֳ���ƽ�����۸���ɢ��ͼ�������ɲ���![]() ��Ϊ���ֳ�ƽ�����۸�
��Ϊ���ֳ�ƽ�����۸�![]() ������ʹ������
������ʹ������![]() �Ļع鷽�̣�����������±�������
�Ļع鷽�̣�����������±�������![]() ��
��![]() ����
����
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
�ٸ��ݻع鷽�����ͼ��������ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
�ڸ����������г���ʹ��8������(��8��)�Ķ��ֳ���ȡ�ɽ��۸�![]() ��Ӷ�𣬶�ʹ��ʱ��8������(����8��)�Ķ��ֳ���ȡ�ɽ��۸�
��Ӷ�𣬶�ʹ��ʱ��8������(����8��)�Ķ��ֳ���ȡ�ɽ��۸�![]() ��Ӷ����ͼ1��ʹ��ʱ��ķ����У��Ը���������е�ֵ��������ĸ���ֵ������2017���������Ϊ�������ݣ���������������г��Գɽ���ÿ������ȡ��ƽ��Ӷ��
��Ӷ����ͼ1��ʹ��ʱ��ķ����У��Ը���������е�ֵ��������ĸ���ֵ������2017���������Ϊ�������ݣ���������������г��Գɽ���ÿ������ȡ��ƽ��Ӷ��
��ע���ٶ���һ������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ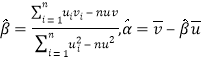 ��
��
�ڲο����ݣ�![]() ��
��
���𰸡���1��![]() ����2����
����2����![]() ����
����![]() ��Ԫ.
��Ԫ.
����������������1����Ƶ�ʷֲ�ֱ��ͼ�ã������������г�2017��ɽ��Ķ��ֳ�ʹ��ʱ����![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ����
����![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ����
����![]() ��
��
��2������![]() ��
��![]() ����
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() �� ����
�� ����![]() ��
��![]() ��
��![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ���ݴ˿ɵ�
���ݴ˿ɵ�![]()
�ڸ��ݢ��еĻع鷽��![]() ��ͼ1���Գɽ��Ķ��ֳ���Ԥ�⣺
��ͼ1���Գɽ��Ķ��ֳ���Ԥ�⣺
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��������������г����ڳɽ���ÿ�����ɻ�õ�ƽ��Ӷ��Ϊ
��������������г����ڳɽ���ÿ�����ɻ�õ�ƽ��Ӷ��Ϊ![]() ��Ԫ.
��Ԫ.
��⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ã������������г�2017��ɽ��Ķ��ֳ�ʹ��ʱ����![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ����
����![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]()
����![]() ��
��
��2������![]() ��
��![]() ����
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ��
��
��Ϊ ��
��
![]()
����![]() ����
����![]() �����Իع鷽��Ϊ
�����Իع鷽��Ϊ![]() ��
��
��![]() ����
����![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]()
�ڸ��ݢ��еĻع鷽��![]() ��ͼ1���Գɽ��Ķ��ֳ���Ԥ�⣺
��ͼ1���Գɽ��Ķ��ֳ���Ԥ�⣺
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]() ��
��
ʹ��ʱ����![]() ��ƽ���ɽ��۸�Ϊ
��ƽ���ɽ��۸�Ϊ![]() ����Ӧ��Ƶ��Ϊ
����Ӧ��Ƶ��Ϊ![]()
���Ը����������г����ڳɽ���ÿ�����ɻ�õ�ƽ��Ӷ��Ϊ
![]()
![]() ��Ԫ.
��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ��
��![]() ��
�� ![]() Ϊ��Ȼ�����ĵ�����.
Ϊ��Ȼ�����ĵ�����.
��1�������ۺ���![]() �ļ�ֵ�����
�ļ�ֵ�����
��2��֤������![]() ��
��![]() ʱ������
ʱ������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪,��ͼ,��ֱ�����![]() ��,�ı���
��,�ı���![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() ��������,
��������,![]() ,��
,��![]() .
.

������֤:![]() ƽ��
ƽ��![]() ;
;
����������![]() ������ֵ;
������ֵ;
�������߶�![]() ���������˵㣩���Ƿ���ڵ�
���������˵㣩���Ƿ���ڵ�![]() ,ʹ��
,ʹ��![]() ��ƽ��
��ƽ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() ;������,д��
;������,д��![]() ��ֵ,��������,˵������.
��ֵ,��������,˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ��
��
��1��������![]() ��
��![]() �����ߵ�б��Ϊ
�����ߵ�б��Ϊ![]() ��������߷�����
��������߷�����
��2����![]() ��������ֵ��
��������ֵ��![]() ����
����![]() ��ȡֵ��Χ����֤����
��ȡֵ��Χ����֤����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ����
����![]() ʱ�����������ʵ��
ʱ�����������ʵ��![]() �����в���ʽ
�����в���ʽ![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() ���е㣬���߶�
���е㣬���߶�![]() ���е�
���е�![]() ��
��![]() ��ƽ���ߣ��ֱ�
��ƽ���ߣ��ֱ�![]() �ڵ�
�ڵ�![]() .
.

��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���y��ex������y��ex���������ύ�㴦�����߷���Ϊy��x+1���������� y��ex������y��x+1���Ϸ������в���ʽex��x+1������������������ں���y��lnx��x��0�����в���ʽ��������
A. lnx��x+1��x��0��B. lnx��1��x��x��0��
C. lnx��x��1��x��0��D. lnx��x��1��x��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() �������ⳤ��Ϊ
�������ⳤ��Ϊ![]() ����
����![]() �ϵ�һ�㣬
�ϵ�һ�㣬![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ���е㣮
���е㣮
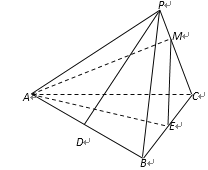
��1����֤: ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ƽ��
ƽ��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com