
(本题满分14分,第1小题6分,第2小题8分)
已知函数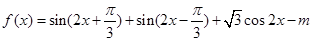 ,x∈R,且f(x)的最大值为1.
,x∈R,且f(x)的最大值为1.
(1) 求m的值,并求f(x)的单调递增区间;
(2) 在△ABC中,角A、B、C的对边a、b、c,若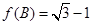 ,且
,且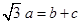 ,试判断△ABC的形状.
,试判断△ABC的形状.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?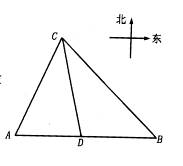
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com