
【题目】已知函数![]() 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当![]() 时,
时,![]() .若关于x的不等式
.若关于x的不等式![]() 只有两个整数解,则实数a的取值范围为_______.
只有两个整数解,则实数a的取值范围为_______.
科目:高中数学 来源: 题型:
【题目】科学家发现某种特别物质的温度![]() (单位:摄氏度)随时间
(单位:摄氏度)随时间![]() (时间:分钟)的变化规律满足关系式:
(时间:分钟)的变化规律满足关系式:![]() (
(![]() ,
,![]() ).
).
(1)若![]() ,求经过多少分钟,该物质的温度为5摄氏度;
,求经过多少分钟,该物质的温度为5摄氏度;
(2)如果该物质温度总不低于2摄氏度,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣axlnx.
(1)当a=1时,求曲线f(x)在x=1处的切线方程;
(2)证明:对于a∈(0,e),函数f(x)在区间(![]() )上单调递增.
)上单调递增.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是一个菱形,三角形PAD是一个等腰三角形,∠BAD=∠PAD=![]() ,点E在线段PC上,且PE=3EC.
,点E在线段PC上,且PE=3EC.
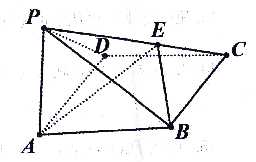
(1)求证:AD⊥PB;
(2)若平面PAD⊥平面ABCD,求二面角E﹣AB﹣P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )
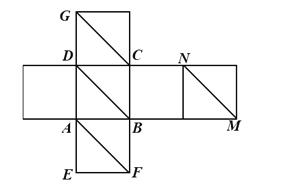
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来。某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图。
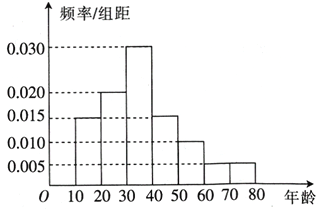
(1)试求这40人年龄的平均数、中位数的估计值;
(2)(i)若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;
(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com