
【题目】在△ABC中,A、B、C的对边分别为a、b、c,己知c﹣b=2bcosA.
(1)若a=2 ![]() ,b=3,求c;
,b=3,求c;
(2)若C= ![]() ,求角B.
,求角B.
【答案】
(1)解:∵c﹣b=2bcosA.
∴由余弦定理可得:c﹣b=2b× ![]() ,整理可得:a2=b2+bc,
,整理可得:a2=b2+bc,
∵a=2 ![]() ,b=3,
,b=3,
∴24=9+3c,解得:c=5.
(2)解:∵C= ![]() ,∴A+B=
,∴A+B= ![]() ,可得sinA=cosB,cosA=sinB,
,可得sinA=cosB,cosA=sinB,
∴c﹣b=2bcosA,由正弦定理可得:sin(A+B)=2sinBcosA+sinB,
可得:sinAcosB+cosAsinB=2sinBcosA+sinB,
解得:cos2B+sin2B=2sin2B+sinB=1,即:2sin2B+sinB﹣1=0,
可得:sinB= ![]() 或﹣1(舍去).即B=
或﹣1(舍去).即B= ![]() .
.
【解析】(1)由余弦定理化简已知等式,整理可得:a2=b2+bc,代入已知即可解得c的值.(2)由题意A+B= ![]() ,可得sinA=cosB,cosA=sinB,由正弦定理化简已知等式可得:2sin2B+sinB﹣1=0,解得sinB,即可求B=
,可得sinA=cosB,cosA=sinB,由正弦定理化简已知等式可得:2sin2B+sinB﹣1=0,解得sinB,即可求B= ![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 的焦距为2.
的焦距为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,过
,过![]() 作
作![]() 轴且与椭圆
轴且与椭圆![]() 交于另一点
交于另一点![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,求证:三点
的右焦点,求证:三点![]() 在同一条直线上.
在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】完成下列进位制之间的转化.
(1)10231(4)=________(10);
(2)235(7)=________(10);
(3)137(10)=________(6);
(4)1231(5)=________(7);
(5)213(4)=________(3);
(6)1010111(2)=________(4).
查看答案和解析>>
科目:高中数学 来源: 题型:
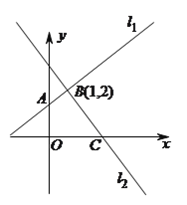
【题目】如图,经过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 和
和![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() ,直线
,直线![]() 交
交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如果![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)试问是否总存在经过![]() ,
, ![]() ,
, ![]() ,
, ![]() 四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
四点的圆?如果存在,求出半径最小的圆的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】滨湖区拟建一主题游戏园,该游戏园为四边形区域ABCD,其中三角形区城ABC为主题活动区,其中∠ACB=60°,∠ABC=45°,AB=12 ![]() m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩.
m;AD、CD为游客通道(不考虑宽度),且∠ADC=120°,通道AD、CD围成三角形区域ADC为游客休闲中心,供游客休憩. 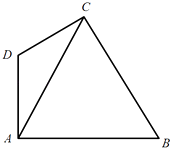
(1)求AC的长度;
(2)记游客通道AD与CD的长度和为L,求L的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年级举办团知识竞赛.![]() 、
、![]() 、
、![]() 、
、![]() 四个班报名人数如下:
四个班报名人数如下:
班别 |
|
|
|
|
人数 | 45 | 60 | 30 | 15 |
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(Ⅰ)求各班参加竞赛的人数;
(Ⅱ)若![]() 班每位参加竞赛的同学对每个题目答对的概率均为
班每位参加竞赛的同学对每个题目答对的概率均为![]() ,求
,求![]() 班恰好有2位同学获得奖品的概率;
班恰好有2位同学获得奖品的概率;
(Ⅲ)若这10个题目,小张同学只有2个答不对,记小张答对的题目数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com