


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
(1) 四面体的四个面是全等三角形的充要条件是该四面体为正四面体;
(2) 有两个侧面是矩形是四棱柱为直棱柱的充要条件;
(3) 三棱锥最多有三个面为直角三角形;
(4) 三棱锥S—ABC的三条侧棱两两互相垂直,P是底面内一点,PS与三条侧棱所成的角分别为α、β、γ,则cos2α+cos2β+cos2γ为定值.其中正确命题个数是( )
(A) 4 (B) 3 (C) 2 (D)1
查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南红河州高中毕业生统一检测理科数学试卷(解析版) 题型:选择题
给出以下四个命题:
(1)在 中, “
中, “ ”是“
”是“ ”的必要而非充分条件;
”的必要而非充分条件;
(2)函数 的最小正周期是
的最小正周期是 ;
;
(3)在 中,若
中,若

 ,则
,则 为钝角三角形;
为钝角三角形;
(4)在同一坐标系中,函数 与函数
与函数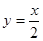 的图象有三个交点
的图象有三个交点
其中正确命题的个数是( )
A. 1  B.
2 C.
3
D. 4
B.
2 C.
3
D. 4
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com