
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为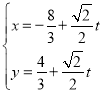 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在平面直角坐标系![]() 中,设直线
中,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.若点
两点.若点![]() 恰为线段
恰为线段![]() 的三等分点,求
的三等分点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知x与y之间的几组数据如表:
x | 1 | 2 | 3 | 4 |
y | 1 | m | n | 4 |
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程分别为![]() ,
,![]() ,
,![]() ,对应的相关系数分别为
,对应的相关系数分别为![]() ,
,![]() ,
,![]() ,下列结论中错误的是( )
,下列结论中错误的是( )
参考公式:线性回归方程![]() 中,其中
中,其中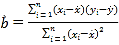 ,
,![]() .相关系数
.相关系数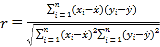 .
.
A.三条回归直线有共同交点B.相关系数中,![]() 最大
最大
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了调查本小区业主对物业服务满意度的真实情况,对本小区业主进行了调查,调查中问了两个问题1:你的手机尾号是不是奇数?问题2:你是否满意物业的服务?调查者设计了一个随机化装置,其中装有大小、形状和质量完全相同的白球和红球,每个被调查者随机从装置中摸到红球和白球的可能性相同,其中摸到白球的业主回答第一个问题,摸到红球的业主回答第二个问题,回答“是”的人往一个盒子中放一个小石子,回答“否”的人什么都不要做由于问题的答案只有“是”和“否”,而且回答的是哪个问题别人并不知道,因此被调查者可以毫无顾虑地给出符合实际情况的答案.已知某小区80名业主参加了问卷,且有47名业主回答了“是”,由此估计本小区对物业服务满意的百分比大约为( )
A.85%B.75%C.63.5%D.67.5%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在圆
在圆![]() 上,且圆
上,且圆![]() 上的所有点均在椭圆
上的所有点均在椭圆![]() 外,若
外,若![]() 的最小值为
的最小值为![]() ,且椭圆
,且椭圆![]() 的长轴长恰与圆
的长轴长恰与圆![]() 的直径长相等,则下列说法正确的是( )
的直径长相等,则下列说法正确的是( )
A.椭圆![]() 的焦距为
的焦距为![]() B.椭圆
B.椭圆![]() 的短轴长为
的短轴长为![]()
C.![]() 的最小值为
的最小值为![]() D.过点
D.过点![]() 的圆
的圆![]() 的切线斜率为
的切线斜率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出:坚决打赢脱贫攻坚战,做到精准扶贫.某县积极引导农民种植一种名贵中药材,从而大大提升了该县村民的经济收入.2019年年底,该机构从该县种植的这种名贵药材的农户中随机抽取了100户,统计了他们2019年因种植,中药材所获纯利润(单位:万元)的情况(假定农户因种植中药材这一项一年最多获利11万元),统计结果如下表所示:
![]()
(1)由表可以认为,该县农户种植中药材所获纯利润Z(单位:万元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 近似为样本方差
近似为样本方差![]() .若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
.若该县有1万户农户种植了该中药材,试估算所获纯利润Z在区间(1.9,8.2)的户数;
(2)为答谢广大农户的积极参与,该调查机构针对参与调查的农户举行了抽奖活动,抽奖规则如下:在一箱子中放置5个除颜色外完全相同的小球,其中红球1个,黑球4个.让农户从箱子中随机取出一个小球,若取到红球,则抽奖结束;若取到黑球,则将黑球放回箱中,让他继续取球,直到取到红球为止(取球次数不超过10次).若农户取到红球,则视为中奖,获得2000元的奖励,若一直未取到红球,则视为不中奖.现农户张明参加了抽奖活动,记他中奖时取球的次数为随机变量X,他取球的次数为随机变量Y.
①证明:![]() 为等比数列;
为等比数列;
②求Y的数学期望.(精确到0.001)
参考数据:![]() .若随机变量
.若随机变量![]() 则
则![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着2022年北京冬奥会的临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放.如图是2012-2018年中国雪场滑雪人数(单位:万人)与同比增长情况统计图则下面结论中正确的是( ).
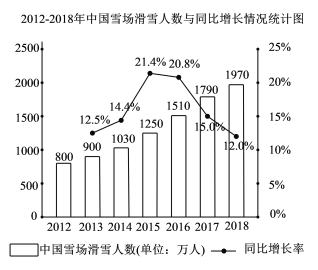
A.2012-2018年,中国雪场滑雪人数逐年增加;
B.2013-2015年,中国雪场滑雪人数和同比增长率均逐年增加;
C.中国雪场2015年比2014年增加的滑雪人数和2018年比2017年增加的滑雪人数均为220万人,因此这两年的同比增长率均有提高;
D.2016-2018年,中国雪场滑雪人数的增长率约为23.4%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节突如其来的新型冠状病毒肺炎在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙两名医生,抽调![]() 、
、![]() 、
、![]() 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士
三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士![]() 被选在第一医院工作的概率为( )
被选在第一医院工作的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为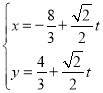 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
(Ⅰ)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在平面直角坐标系![]() 中,设直线
中,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点.若点
两点.若点![]() 恰为线段
恰为线段![]() 的三等分点,求
的三等分点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
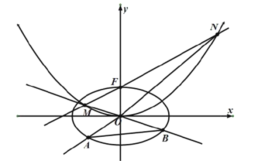
【题目】如图,已知椭圆![]() ,点
,点![]() 是抛物线
是抛物线![]() 的焦点,过点F作直线
的焦点,过点F作直线![]() 交抛物线于M,N两点,延长
交抛物线于M,N两点,延长![]() ,
,![]() 分别交椭圆于A,B两点,记
分别交椭圆于A,B两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,
,![]() .
.
(1)求![]() 的值及抛物线的准线方程;
的值及抛物线的准线方程;
(2)求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com