练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆过点，其长轴、焦距和短轴的长的平方依次成等差数列直线l与x轴正半轴和y轴分别交于点Q、P，与椭圆分别交于点M、N，各点均不重合且满足．

    求椭圆的标准方程；

    若，试证明：直线l过定点并求此定点．

    【答案】（1）；（2）见解析

    【解析】

    （1）由已知条件推导出，，由此能求出椭圆的方程．

    （2）由题意设，，，，设l方程为，由已知条件推导出，，由此能证明直线l过定点并能求出此定点．

    解：椭圆过点，

    ，设焦距为2c，

    长轴、焦距和短轴的长的平方依次成等差数列，

    ，又

    解得

    椭圆的方程为

    由题意设，，，，

    设l方程为，

    由，知

    ，由题意，，

    同理由知，，

    ，，

    联立，得，

    需

    且有，

    代入得，，

    直线与轴正半轴和轴分别交于点Q、P，

    由题意，满足，

    得方程为，过定点，即为定点

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

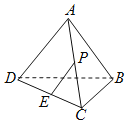
    【题目】已知三棱锥A﹣BCD的所有棱长均相等，E为DC的中点，若点P为AC中点，则直线PE与平面BCD所成角的正弦值为_____，若点Q在棱AC所在直线上运动，则直线QE与平面BCD所成角正弦值的最大值为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,四棱锥的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=,E为PC的中点.

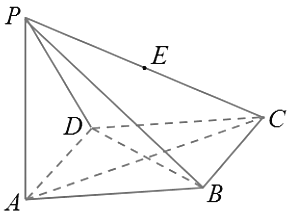
    (1)求直线DE与平面PAC所成角的大小；

    (2)求二面角E-AD-C平面角的正切值；

    (3)在线段PC上是否存在一点M,使PC⊥平面MBD成立.如果存在,求出MC的长；如果不存在,请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABCA1B1C1中，∠ABC＝，D是棱AC的中点，且AB＝BC＝BB1＝2.

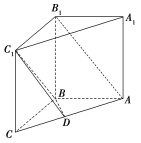
    (1)求证：AB1∥平面BC1D；

    (2)求异面直线AB1与BC1的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

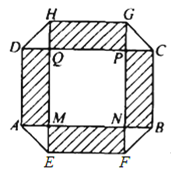
    【题目】如图，居民小区要建一座八边形的休闲场所，它的主体造型平面图是由两个相同的矩形和构成的面积为的十字形地域，计划在正方形上建一座花坛，造价为元/；在四个相同的矩形（图中阴影部分）上铺上花岗岩地坪，造价为元/；再在四个空角（图中四个三角形，如）上铺草坪，造价为元/

    （1）设总造价为（单位：元），长为（单位：），试求出关于的函数关系式，并求出定义域；

    （2）当长取何值时，总造价最小，并求出这个最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

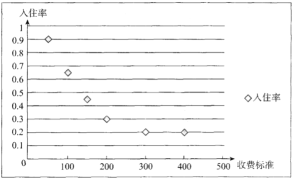
    【题目】近年来，随着互联网技术的快速发展，共享经济覆盖的范围迅速扩张，继共享单车、共享汽车之后，共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”，为了确定未来发展方向，此创业者对该景区附近六家“农家乐”跟踪调查了天.得到的统计数据如下表，为收费标准（单位：元/日），为入住天数（单位：），以频率作为各自的“入住率”，收费标准与“入住率”的散点图如图

    x

    50

    100

    150

    200

    300

    400

    t

    90

    65

    45

    30

    20

    20

    （1）若从以上六家“农家乐”中随机抽取两家深入调查，记为“入住率”超过的农家乐的个数，求的概率分布列；

    （2）令，由散点图判断与哪个更合适于此模型（给出判断即可，不必说明理由）？并根据你的判断结果求回归方程.（结果保留一位小数）

    （3）若一年按天计算，试估计收费标准为多少时，年销售额最大？（年销售额入住率收费标准）

    参考数据：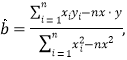

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】双曲线C：1（a＞0，b＞0）的左右焦点为F1，F2（|F1F2|＝2c），以坐标原点O为圆心，以c为半径作圆A，圆A与双曲线C的一个交点为P，若三角形F1PF2的面积为a2，则C的离心率为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

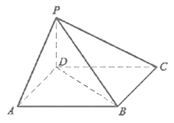
    【题目】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马．如图所示，在阳马中，底面．

    （1）若，斜梁与底面所成角为，求立柱的长（精确到）；

    （2）证明：四面体为鳖臑；

    （3）若，，，为线段上一个动点，求面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体中，E是棱的中点.

    (1)画出平面与平面的交线；

    (2)在棱上是否存在一点F，使得∥平面若存在,指明点F的位置；若不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案