
【题目】双曲线![]() 的一个焦点
的一个焦点![]() 恰好与抛物线
恰好与抛物线![]() 的焦点
的焦点![]() 重合,且两曲线的一个交点为
重合,且两曲线的一个交点为![]() ,若
,若![]() ,则双曲线的方程为( )
,则双曲线的方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加
平均增加![]() 个单位;
个单位;
③线性回归方程![]() 必过
必过![]() );
);
④在一个![]() 列联表中,由计算得
列联表中,由计算得![]() ,则有
,则有![]() 以上的把握认为这两个变量间有关系.
以上的把握认为这两个变量间有关系.
其中错误的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是使得解析式有意义的x集合,如果对于定义域内的任意实数x,函数值均为正,则称此函数为“正函数”.
的定义域是使得解析式有意义的x集合,如果对于定义域内的任意实数x,函数值均为正,则称此函数为“正函数”.
(1)证明函数![]() 是“正函数”;
是“正函数”;
(2)如果函数![]() 不是“正函数”,求正数a的取值范围.
不是“正函数”,求正数a的取值范围.
(3)如果函数 是“正函数”,求正数a的取值范围.
是“正函数”,求正数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有8名马拉松比赛志愿者,其中志愿者![]() ,
,![]() ,
,![]() 通晓日语,
通晓日语,![]() ,
,![]() ,
,![]() 通晓俄语,
通晓俄语,![]() ,
,![]() 通晓英语,从中选出通晓日语、俄语和英语的志愿者各1名,组成一个小组.
通晓英语,从中选出通晓日语、俄语和英语的志愿者各1名,组成一个小组.
![]() 列出基本事件;
列出基本事件;
![]() 求
求![]() 被选中的概率;
被选中的概率;
![]() 求
求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 都是各项为正数的数列,且
都是各项为正数的数列,且![]() ,
,![]() .对任意的正整数n,都有
.对任意的正整数n,都有![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若存在p>0,使得集合M=![]() 恰有一个元素,求实数
恰有一个元素,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
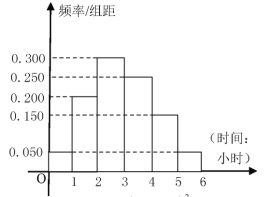
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附: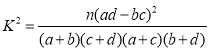
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的命题是( )
A.标准差越小,则反映样本数据的离散程度越大
B.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,则预报变量
每增加1个单位时,则预报变量![]() 减少0.4个单位
减少0.4个单位
C.对分类变量![]() 与
与![]() 来说,它们的随机变量
来说,它们的随机变量![]() 的观测值
的观测值![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
D.在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com