
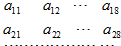 (理)64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等).若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.则a81a82…a88…aij=j($\frac{1}{2}$)i.
(理)64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等).若a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.则a81a82…a88…aij=j($\frac{1}{2}$)i. 分析 设第一行的公差为d,进而根据a24=1,a32=$\frac{1}{4}$,利用等差数列和等比数列的通项公式可得方程组求得q和d,进而求得aij.
解答 解:设第一行的公差为d,依题意可知$\left\{\begin{array}{l}{(\frac{1}{2}+d){q}^{2}=\frac{1}{4}}\\{(\frac{1}{2}+3d)q=1}\end{array}\right.$,解得q=$\frac{1}{2}$,d=$\frac{1}{2}$
∴aij=[$\frac{1}{2}$+(j-1)$\frac{1}{2}$]($\frac{1}{2}$)i-1=j($\frac{1}{2}$)i.
故答案为:j($\frac{1}{2}$)i.
点评 本题主要考查了等差数列和等比数列的通项公式.本题主要考查了学生对等差数列和等比数列的理解和灵活运用.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 31 | B. | $\frac{31}{16}$ | C. | 11 | D. | $\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com