练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图某几何体的三视图是直角边长为1的三个等腰直角三角形，则该几何体的外接球的表面积为（ ）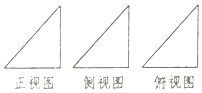
    A.
    B.
    C.
    D.3π

    【答案】D
    【解析】解：∵该几何体的三视图是直角边长为1的三个等腰直角三角形，∴该几何体为从底面直角顶点出发的三条棱两两垂直的三棱锥，可将其补成一个边长为1的正方体，
    则该几何体的外接球就是补成的正方体的外接球，
    ∵补成的正方体的对角线长l= = 为其外接球的直径d，
    ∴外接球的表面积S=πd2=3π，
    即该几何体的外接球的表面积为3π，
    故选：D．
    【考点精析】本题主要考查了由三视图求面积、体积和球内接多面体的相关知识点，需要掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积；球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，平面A1BC⊥侧面A1ABB1 ， 且AA1=AB=2．

    （1）求证：AB⊥BC；
    （2）若直线AC与平面A1BC所成的角为 ，求锐二面角A﹣A1C﹣B的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在Z上的函数f（x），对任意x，y∈Z，都有f（x+y）+f（x﹣y）=4f（x）f（y）且f（1）= ，则f（0）+f（1）+f（2）+…+f（2017）= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，输出S的值为（ ）

    A.45
    B.55
    C.66
    D.110

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场进行有奖促销活动，顾客购物每满500元，可选择返回50元现金或参加一次抽奖，抽奖规则如下：从1个装有6个白球、4个红球的箱子中任摸一球，摸到红球就可获得100元现金奖励，假设顾客抽奖的结果相互独立．
    （Ⅰ）若顾客选择参加一次抽奖，求他获得100元现金奖励的概率；
    （Ⅱ）某顾客已购物1500元，作为商场经理，是希望顾客直接选择返回150元现金，还是选择参加3次抽奖？说明理由；
    （Ⅲ）若顾客参加10次抽奖，则最有可能获得多少现金奖励？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn ， a1=1，满足 ， ， ．
    （1）求证：数列 为等比数列；
    （2）求数列{Sn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正四棱锥P﹣ABCD中，PA=AB=a，E是棱PC的中点．
    （1）求证：PC⊥BD；
    （2）求直线BE与PA所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市A（看做一点）的东偏南θ角方向 ，300km的海面P处，并以20km/h的速度向西偏北45°方向移动．台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大．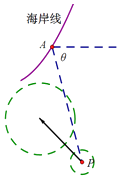
    （1）问10小时后，该台风是否开始侵袭城市A，并说明理由；
    （2）城市A受到该台风侵袭的持续时间为多久？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图的程序框图表示的算法中，输入三个实数a，b，c，要求输出的x是这三个数中最大的数，那么在空白的判断框中，应该填入（ ）

    A.x＞c
    B.c＞x
    C.c＞b
    D.c＞a

    查看答案和解析>>

    同步练习册答案