练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线的顶点在坐标原点，准线方程为，为抛物线的焦点，点为直线上任意一点，以为圆心，为半径的圆与抛物线的准线交于、两点，过、分别作准线的垂线交抛物线于点、.

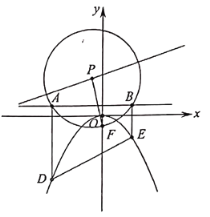
    （1）求抛物线的方程；

    （2）证明：直线过定点，并求出定点的坐标.

    【答案】（1）；（2）证明见解析，定点.

    【解析】

    （1）设抛物线的标准方程为，根据抛物线的准线方程可求得的值，由此可求得抛物线的方程；

    （2）设点的坐标为，求出圆的方程，与直线方程联立，可得出关于、的二次方程，并设点、，可列出韦达定理，并求得直线的方程，进而可求得直线所过定点的坐标.

    （1）设抛物线的标准方程为，

    依题意，，抛物线的方程为；

    （2），设，则，，

    于是圆的方程为，

    令，得，①

    设、，由①式得，，②

    直线的斜率为，

    则直线的方程为，

    代入②式就有，

    因为上式对恒成立，故，即直线过定点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在棱长为1的正方体中，MN分别是棱的中点，P是体对角线上一点，满足，则平面MNP截正方体所得截面周长为_______

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面为正方形，.

    （1）证明：面⊥面；

    （2）若与底面所成的角为， ，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线上一点到焦点的距离为，过作两条互相垂直的直线和，其中斜率为与抛物线交于A，B，与y轴交于C，点Q满足：

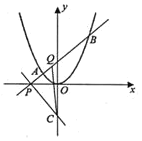
    （1）求抛物线的方程；

    （2）求三角形PQC面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）当时，求证：；

    （2）若有三个零点时，求的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）.

    （1）求的极值；

    （2）设,若当时,恒成立,求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，曲线的参数方程为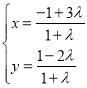（为参数，且）.以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）已知点P的极坐标为，Q为曲线上的动点，求的中点M到曲线的距离的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若在处的切线方程为，求实数的值；

    （2）证明：当时，在上有两个极值点；

    （3）设，若在上是单调减函数（为自然对数的底数），求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某民航部门统计的2019年春运期间12个城市售出的往返机票的平均价格以及相比上年同期变化幅度的数据统计图表如图所示，根据图表，下面叙述不正确的是( )

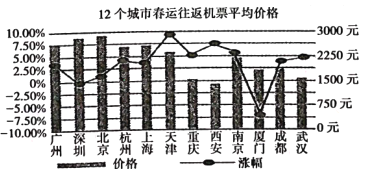
    A. 同去年相比，深圳的变化幅度最小且厦门的平均价格有所上升

    B. 天津的平均价格同去年相比涨幅最大且2019年北京的平均价格最高

    C. 2019年平均价格从高到低居于前三位的城市为北京、深圳、广州

    D. 同去年相比，平均价格的涨幅从高到低居于前三位的城市为天津、西安、南京

    查看答案和解析>>

    同步练习册答案