
【题目】设函数![]() (
(![]() R).
R).
(1)求函数![]() 在R上的最小值;
在R上的最小值;
(2)若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)若方程![]() 在
在![]() 上有四个不相等的实数根,求
上有四个不相等的实数根,求![]() 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某农业合作社生产了一种绿色蔬菜共![]() 吨,如果在市场上直接销售,每吨可获利
吨,如果在市场上直接销售,每吨可获利![]() 万元;如果进行精加工后销售,每吨可获利
万元;如果进行精加工后销售,每吨可获利![]() 万元,但需另外支付一定的加工费,总的加工
万元,但需另外支付一定的加工费,总的加工![]() (万元)与精加工的蔬菜量
(万元)与精加工的蔬菜量![]() (吨)有如下关系:
(吨)有如下关系: 设该农业合作社将
设该农业合作社将![]() (吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为
(吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为![]() (万元).
(万元).
(1)写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当精加工蔬菜多少吨时,总利润最大,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)已知![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值;
的值;
(2)已知![]() ,设
,设![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两根,且
的两根,且![]() ,求实数
,求实数![]() 的值;
的值;
(3)已知![]() 满足
满足![]() ,且关于
,且关于![]() 的方程
的方程![]() 的两实数根分别在区间
的两实数根分别在区间![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
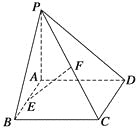
求证:(1)CD⊥PD;(2)EF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两队学生参加“知识联想”抢答赛,比赛规则:①主持人依次给出两次提示,第一次提示后答对得2分,第二次提示后答对得1分,没抢到或答错者不得分;②主持人给出第一个提示后开始抢答,第一轮抢答出错失去第二轮答题资格;③每局比赛分两轮,若第一轮抢答者给出正确答案,则此局比赛结束,若第一轮答题者答错,主持人提示后另一队直接答题。如果甲、乙两队抢到答题权机会均等,并且势均力敌,第一个提示后答对概率均为![]() ;第二个提示后答对概率均为
;第二个提示后答对概率均为![]() ,
,![]() 为甲队在一局比赛中的分.
为甲队在一局比赛中的分.
(1)求甲在一局比赛中得分的分布列;
(2)若比赛共4局,求甲4局比赛中至少得6分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点
中,点![]() 在平面
在平面![]() 内运动,使得二面角
内运动,使得二面角![]() 的平面角与二面角
的平面角与二面角![]() 的平面角互余,则点
的平面角互余,则点![]() 的轨迹是( )
的轨迹是( )

A. 一段圆弧 B. 椭圆的一部分 C. 抛物线 D. 双曲线的一支
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com