
【题目】如图是正四面体的平面展开图,![]() 分别是
分别是![]() 的中点,在这个正四面体中:①
的中点,在这个正四面体中:①![]() 与
与![]() 平行;②
平行;②![]() 与
与![]() 为异面直线;③
为异面直线;③![]() 与
与![]() 成60°角;④
成60°角;④![]() 与
与![]() 垂直.以上四个命题中,正确命题的个数是( )
垂直.以上四个命题中,正确命题的个数是( )
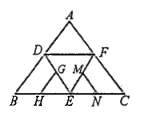
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】分析:正四面体的平面展开图复原为正四面体A(B、C)﹣DEF,
①,依题意,MN∥AF,而DE与AF异面,从而可判断DE与MN不平行;
②,假设BD与MN共面,可得A、D、E、F四点共面,导出矛盾,从而可否定假设,肯定BD与MN为异面直线;
③,依题意知,GH∥AD,MN∥AF,∠DAF=60°,于是可判断GH与MN成60°角;
④,连接GF,那么A点在平面DEF的射影肯定在GF上,通过线面垂直得到线线垂直.
详解:将正四面体的平面展开图复原为正四面体A(B、C)﹣DEF,如图:
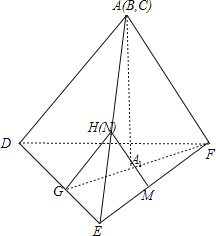
对于①,M、N分别为EF、AE的中点,则MN∥AF,而DE与AF异面,故DE与MN不平行,故①错误;
对于②,BD与MN为异面直线,正确(假设BD与MN共面,则A、D、E、F四点共面,与ADEF为正四面体矛盾,故假设不成立,故BD与MN异面);
对于③,依题意,GH∥AD,MN∥AF,∠DAF=60°,故GH与MN成60°角,故③正确;
对于④,连接GF,A点在平面DEF的射影A1在GF上,∴DE⊥平面AGF,DE⊥AF,
而AF∥MN,∴DE与MN垂直,故④正确.
综上所述,正确命题的序号是②③④,
故答案为:②③④.


科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.

(1)求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某片森林原来面积为a,计划每年砍伐的森林面积是上一年年末森林面积的p%,当砍伐到原来面积的一半时,所用时间是10年,已知到2018年年末,森林剩余面积为原来面积的![]() ,为保护生态环境,森林面积至少要保留原来面积的
,为保护生态环境,森林面积至少要保留原来面积的![]() .
.
(1)求每年砍伐面积的百分比P%;
(2)到2018年年末,该森林已砍伐了多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元), ![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(Ⅰ)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.5,求
”的频率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com