
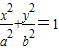 的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若
的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若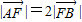 ,则椭圆的离心率e= .
,则椭圆的离心率e= . 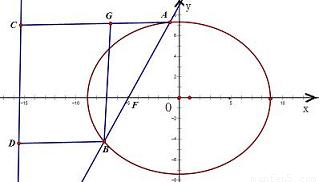 解:如图,设设椭圆的左准线为l,过A点作AC⊥l于C,
解:如图,设设椭圆的左准线为l,过A点作AC⊥l于C,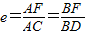 ,
,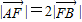
 …②
…②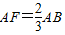
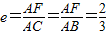



 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源:江西省六校2010届高三下学期联考数学文科试题 题型:022
过椭圆![]() 的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若
的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若![]() ,则椭圆的离心率e=________.
,则椭圆的离心率e=________.
查看答案和解析>>
科目:高中数学 来源:2010年广东省广州市越秀区高考数学一轮双基小题练习(06)(解析版) 题型:解答题
 的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若
的左焦点F且倾斜角为60°的直线交椭圆于A、B两点,若 ,则椭圆的离心率e= .
,则椭圆的离心率e= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com