
【题目】已知公差不为0的等差数列{an}的首项a1为a(a∈R).设数列的前n项和为Sn,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列{an}的通项公式及Sn;
(2)记![]() ,
,![]() .当n≥2时,求An与Bn.
.当n≥2时,求An与Bn.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() 的方程为
的方程为![]() ,平面内两定点
,平面内两定点![]() 、
、![]() .当
.当![]() 的半径取最小值时:
的半径取最小值时:
(1)求出此时![]() 的值,并写出
的值,并写出![]() 的标准方程;
的标准方程;
(2)在![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的另外一个点
的另外一个点![]() ,使得对于
,使得对于![]() 上任意一点
上任意一点![]() ,总有
,总有![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明你的理由;
的坐标,若不存在,请说明你的理由;
(3)在第(2)问的条件下,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1 , l2分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(2)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=4,点P为直线x+2y﹣9=0上一动点,过点P向圆C引两条切线PA、PB,A、B为切点,则直线AB经过定点( )
A.![]()
B.![]()
C.(2,0)
D.(9,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ⊥平面
⊥平面![]() ,底面
,底面![]() 为正方形,
为正方形,![]() 为
为![]() 的中点,
的中点,![]() .
.
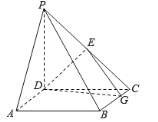
(1)求证:![]() ;
;
(2)![]() 边上是否存在一点
边上是否存在一点![]() ,使得
,使得![]() //平面
//平面![]() ?若存在,求
?若存在,求![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
,曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直. (Ⅰ)求a的值;
(Ⅱ)若对于任意的x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的取值范围;
(Ⅲ)求证:ln(4n+1)≤16 ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校按分层抽样的方法从高中三个年级抽取部分学生调查,从三个年级抽取人数的比例为如图所示的扇形面积比,已知高二年级共有学生1 200人,并从中抽取了40人.

(1)该校的总人数为多少?(2)三个年级分别抽取多少人?
(3)在各层抽样中可采取哪种抽样方法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com