
【题目】已知二次函数![]() 满足
满足![]()
(1)求![]() 的解析式;(2)作出函数
的解析式;(2)作出函数![]() 的图像,并写出其单调区间;
的图像,并写出其单调区间;
(3)求![]() 在区间
在区间![]() (
(![]() )上的最小值。
)上的最小值。
【答案】(1)![]() ;(2)单调递增区间为
;(2)单调递增区间为![]() ,
,![]() ; 单调递减区间为
; 单调递减区间为![]() ,
,![]() ;(3)
;(3)![]() 时,
时, ![]() 最小值为
最小值为![]() ;
; ![]() 时,
时, ![]() 最小值为
最小值为![]() ;
; ![]() 时,最小值为
时,最小值为![]() 。
。
【解析】试题分析:(1)换元法得到![]() ,代入
,代入![]() =
=![]() ;(2)根据表达式,零点分区间,分段画出图像即可;(3)根据第一问的表达式这是轴定区间动的问题,讨论轴和区间的关系即可。
;(2)根据表达式,零点分区间,分段画出图像即可;(3)根据第一问的表达式这是轴定区间动的问题,讨论轴和区间的关系即可。
(1)令![]() 则
则![]() ,
,
![]()
![]() =
=![]() =
=![]()
![]()
![]()
(2)

由图像可知:| ![]() |的单调递增区间为
|的单调递增区间为![]() ;
;
单调递减区间为![]() ,
,![]()
(3)![]() =
=![]()
开口向上,对称轴为![]()
当![]() 时,
时, ![]() 在
在![]() 上为增函数
上为增函数
所以![]() 时y有最小值为
时y有最小值为![]() ;
;
当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上先减后增,
上先减后增,
所以![]() 时y有最小值为
时y有最小值为![]()
当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上为减函数
上为减函数
所以![]() 时y有最小值为
时y有最小值为![]() ;
;
综上所述: ![]() 时,
时, ![]() 最小值为
最小值为![]() ;
; ![]() 时,
时, ![]() 最小值为
最小值为![]() ;
;
![]() 时,最小值为
时,最小值为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.
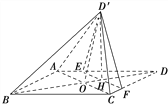
(1)证明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱锥D′ABCFE的体积.
,求五棱锥D′ABCFE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xln x-(x-1)(ax-a+1)(a∈R).
(1)若a=0,判断函数f(x)的单调性;
(2)若x>1时,f(x)<0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 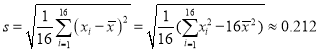 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com