
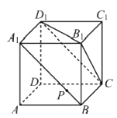
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上移动,有下列判断:①平面
上移动,有下列判断:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③三棱锥
;③三棱锥![]() 的体积不变;④
的体积不变;④![]() 平面
平面![]() .其中,正确的是______.(把所有正确的判断的序号都填上)
.其中,正确的是______.(把所有正确的判断的序号都填上)
【答案】①②③
【解析】
①在正方体中可证平面![]() 平面
平面![]() ,又点
,又点![]() 在线段
在线段![]() 上移动,所以平面
上移动,所以平面![]() 平面
平面![]() ,所以①正确;
,所以①正确;
②先证![]() 平面
平面![]() ,再根据面面垂直的判定定理可证平面
,再根据面面垂直的判定定理可证平面![]() 平面
平面![]() ,所以②正确;
,所以②正确;
③根据![]() 平面
平面![]() ,可得三棱锥
,可得三棱锥![]() 的体积不变,所以③正确;
的体积不变,所以③正确;
④由![]() 平面
平面![]() ,而
,而![]() 与
与![]() 交于
交于![]() ,可得④不正确.
,可得④不正确.
①因为在正方体中有![]() , ,且
, ,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,同理得
,同理得![]() 平面
平面![]() ,
,
又![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
又点![]() 在线段
在线段![]() 上移动,所以平面
上移动,所以平面![]() 平面
平面![]() ,所以①正确;
,所以①正确;
②因为![]() 平面
平面![]() ,所以
,所以![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,
因为![]() ,根据三垂线定理可得
,根据三垂线定理可得![]() ,
,
同理可得![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,所以②正确;
,所以②正确;
③由①知![]() 平面
平面![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为定值,所以三棱锥
的距离为定值,所以三棱锥![]() 的体积不变,所以③正确;
的体积不变,所以③正确;
④由②知![]() 平面
平面![]() ,而
,而![]() 与
与![]() 交于
交于![]() ,所以
,所以![]() 与平面
与平面![]() 不垂直,所以④不正确。
不垂直,所以④不正确。
故答案为:①②③


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() 将函数
将函数![]() 图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移
图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)当![]() ,求实数
,求实数![]() 与正整数
与正整数![]() ,使
,使![]() 在
在![]() 恰有2019个零点.
恰有2019个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
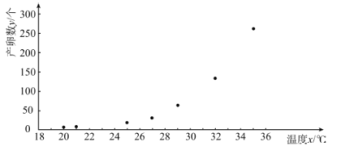
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为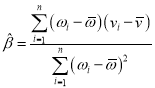 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】刘徽《九章算术商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
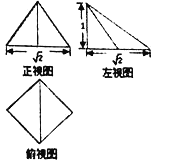
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P–ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为
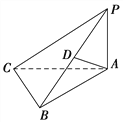
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑.如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
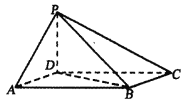
(1)求证:![]() 平面
平面![]() .试判断四面体
.试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(2)若![]() ,求点A到平面
,求点A到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com