已知在等差数列{an}中,a2、a3、a5分别是等比数列{cn}的第4项、第3项、第2项,且a2=8,公差d≠0.
(1)求等比数列{cn}的通项;
(2)设bn=log2cn,求数列{|bn|}的前n项和Tn.
解:(1)由题意知
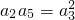
,即8×(8+3d)=(8+d)
2,(2分)
解得d=8或d=0(舍去,∵d≠0),∴a
3=16,a
5=32.
则c
2=32,c
3=16,c
4=8,(4分)
∵|c
n|是等比数列,
∴公比
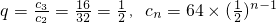
.(6分)
(2)∵
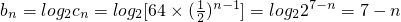
,(7分)
∴
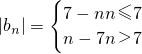
,(9分)
则当n≤7时,
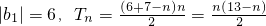
;
当n>7时,
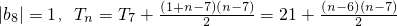
.(11分)
故
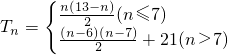
(12分)
分析:(1)利用等差数列{a
n}中,a
2、a
3、a
5分别是等比数列{c
n}的第4项、第3项、第2项,且a
2=8,列出关系式,求出公差,求出等比数列{c
n}的公比,然后求出它的通项;
(2)利用(1),求出b
n=log
2c
n,得到数列{|b
n|}的通项公式,然后求解数列{|b
n|}的前n项和T
n.
点评:本题考查数列通项公式的求法,数列求和的方法,考查计算能力.

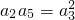 ,即8×(8+3d)=(8+d)2,(2分)
,即8×(8+3d)=(8+d)2,(2分)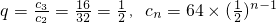 .(6分)
.(6分)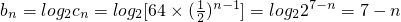 ,(7分)
,(7分)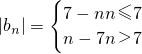 ,(9分)
,(9分)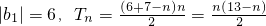 ;
;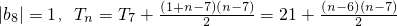 .(11分)
.(11分)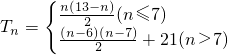 (12分)
(12分)
