分析:(1)采用迭加法,利用递推关系a
n+1-a
n=2n,代入变式a
n=a
1+(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)即可求出a
n(2)采用叠乘法,由
=,即可导出每一项与前一项的比值,然后代入变式a
n=a
1×
×
×
…×
×
即可求出a
n(3)形如a
n+1=ka
n+h(k,h常数)的形式的递推公式求a
n通项时采用构造法,即将数列构造成一个以k为公比的等比数列,即∵
an+1=an+1∴an+1-2=(an-2)∴{an-2}是首项为a
1-2=-1,公比为
的等比数列,由此求出a
n-2的通项后解出a
n即为所求.
解答:解:(1)∵a
n+1=a
n+2n,∴a
n+1-a
n=2n,
∴a
n=a
1+(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)
=1+2×1+2×2+…+2×(n-1)=1+n×(n-1)=n
2-n+1
(2)∵
=,∴
a
n=a
1×
×
×
…×
×
=1×
×
×
…×
×
=
又解:由题意,(n+1)a
n+1=na
n对一切自然数n成立,
∴na
n=(n-1)a
n-1═1•a
1=1,
∴
an=.
(3)∵
an+1=an+1∴an+1-2=(an-2)∴{an-2}是首项为a
1-2=-1
公比为
的等比数列,
∴
a n-2=-1•()n-1,∴
an=2-()n-1.
点评:本例主要复习求通项公式的几种方法:迭加法、迭乘法、构造法;属于数列求通项的重要方法,难度适中,难度系数为0.5



![]() an(n∈N+)
an(n∈N+)![]() (n∈N+)
(n∈N+) an(n∈N*);
an(n∈N*);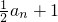 (n∈N*).
(n∈N*).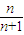 an(n∈N*);
an(n∈N*); (n∈N*).
(n∈N*).