
【题目】某电脑公司有5名产品推销员,其工作年限与年推销金额的数据如表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
![]() 求年推销金额y关于工作年限x的线性回归方程;
求年推销金额y关于工作年限x的线性回归方程;
![]() 判断变量x与y之间是正相关还是负相关;
判断变量x与y之间是正相关还是负相关;
![]() 若第6名推销员的工作年限是11年,试估计他的年推销金额.
若第6名推销员的工作年限是11年,试估计他的年推销金额.
(参考数据![]() ,
,![]() ,
,
参考公式:线性回归方程![]() 中
中![]() ,
,![]() ,其中
,其中![]() 为样本平均数)
为样本平均数)
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市![]() 年
年![]() 月
月![]() 日至
日至![]() 日的空气质量指数趋势图,某人随机选择
日的空气质量指数趋势图,某人随机选择![]() 年
年![]() 月
月![]() 日至
日至![]() 月
月![]() 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留![]() 天.
天.

(1)求此人到达当日空气质量指数大于![]() 的概率;
的概率;
(2)设![]() 是此人停留期间空气质量指数小于
是此人停留期间空气质量指数小于![]() 的天数,求
的天数,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)函数![]() 在
在![]() 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
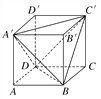
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户,为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元)
(I)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com