
分析 (1)利用余弦定理、三角形的面积公式,结合条件,即可求sinC的值;
(2)由余弦定理得到a2,b2的表达式,两者作差整理即$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$=$\frac{acosB-bcosA}{c}$,再正弦定理将等式右边的a,b,c换成sinA,sinB,sinC来表示,逆用正弦的差角公式即可得出结论.
解答 (1)解:由余弦定理:c2=a2+b2-2abcosC,
∴$S=\frac{1}{2}absinC={({a+b})^2}-{a^2}-{b^2}+2abcosC$,
∴sinC=4cosC+4,
又∵sin2C+cos2C=1,∴17sin2C-8sinC=0,∴sinC=0或$sinC=\frac{8}{17}$
又∵C∈(0,π),∴sinC≠0,∴$sinC=\frac{8}{17}$;
(2)证明:由余弦定理a2=b2+c2-2bccosA,b2=a2+c2-2accosB,
∴a2-b2=b2-a2-2bccosA+2accosB整理得$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$=$\frac{acosB-bcosA}{c}$
依正弦定理,有$\frac{{a}^{2}-{b}^{2}}{{c}^{2}}$=$\frac{acosB-bcosA}{c}$=$\frac{sinAcosB-sinBcosA}{sinC}$=$\frac{sin(A-B)}{sinC}$.
点评 本小题主要考查三角形的正弦定理、余弦定理等基础知识,考查三角函数简单的变形技能.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 x | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| 人数 Y/万人 | 55 196 | 56 300 | 57 482 | 58 796 | 60 266 | 61 560 | 62 828 | 64 563 | 65 994 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 自2008年起,每年的生活垃圾无害化处理量和年份代码正相关 | |
| B. | 自2008年起,每年的生活垃圾无害化处理量大约增加0.10万吨 | |
| C. | 由此模型可知2016年该地区生活垃圾无害化处理量是1.82万吨 | |
| D. | 由此模型预测出2017年该地区生活垃圾无害化处理量约为1.92万吨 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
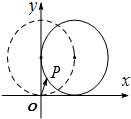 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )| A. | (1-sin1,1-cos1) | B. | (1+sin1,1-cos1) | C. | (1-sin1,1+cos1) | D. | (1+sin1,1+cos1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com