
如图, 为坐标原点,椭圆
为坐标原点,椭圆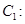
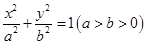 的左右焦点分别为
的左右焦点分别为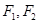 ,离心率为
,离心率为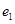 ;双曲线
;双曲线
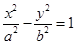 的左右焦点分别为
的左右焦点分别为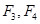 ,离心率为
,离心率为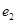 ,已知
,已知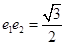 ,且
,且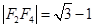 .
.
(1)求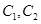 的方程;
的方程;
(2)过 点作
点作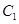 的不垂直于
的不垂直于 轴的弦
轴的弦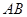 ,
,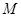 为
为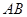 的中点,当直线
的中点,当直线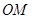 与
与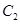 交于
交于 两点时,求四边形
两点时,求四边形 面积的最小值.
面积的最小值.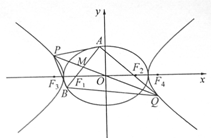
(1) 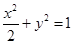
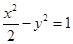 (2)
(2)
解析试题分析:(1)利用椭圆和双曲线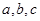 之间的关系可以用
之间的关系可以用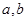 分别表示双曲线和椭圆的离心率和焦点,由题目
分别表示双曲线和椭圆的离心率和焦点,由题目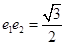 和
和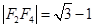 即可得到
即可得到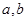 之间的两个方程,联立方程消元即可求出
之间的两个方程,联立方程消元即可求出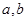 的值,得到双曲线和椭圆的标准方程.
的值,得到双曲线和椭圆的标准方程.
(2)利用(1)求出焦点 的坐标,设出弦
的坐标,设出弦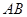 的直线的方程
的直线的方程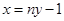 ,联立直线与椭圆消
,联立直线与椭圆消 得到关于
得到关于 的一元二次方程,再利用根与系数的关系得到
的一元二次方程,再利用根与系数的关系得到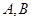 两点纵坐标之间的和与积,进而得到
两点纵坐标之间的和与积,进而得到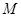 点的纵坐标带入AB直线即可得到
点的纵坐标带入AB直线即可得到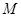 的横坐标,进而求出直线
的横坐标,进而求出直线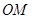 的方程,即为直线
的方程,即为直线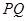 的方程,联立直线
的方程,联立直线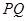 的方程
的方程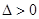 得到
得到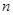 的取值范围和求出点
的取值范围和求出点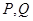 的坐标得到
的坐标得到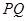 的长度,利用点到直线的距离得到
的长度,利用点到直线的距离得到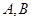 到直线
到直线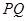 的距离表达式,进而用
的距离表达式,进而用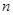 表示四边形的面积,利用不等式的性质和
表示四边形的面积,利用不等式的性质和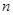 的取值范围即可得到面积的最小值.
的取值范围即可得到面积的最小值.
(1)由题可得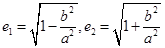 ,且
,且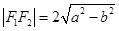 ,因为
,因为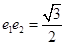 ,且
,且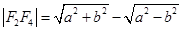 ,所以
,所以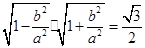 且
且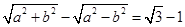
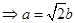 且
且 ,所以椭圆
,所以椭圆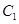 方程为
方程为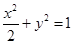 ,双曲线
,双曲线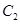 的方程为
的方程为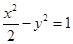 .
.
(2)由(1)可得 ,因为直线
,因为直线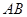 不垂直于
不垂直于 轴,所以设直线
轴,所以设直线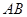 的方程为
的方程为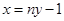 ,联立直线与椭圆方程可得
,联立直线与椭圆方程可得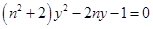 ,则
,则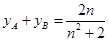 ,
,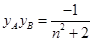 ,则
,则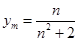 ,因为
,因为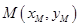 在直线
在直线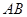 上,所以
上,所以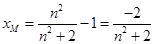 ,则直线
,则直线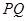 的方程为
的方程为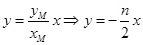 ,联立直线
,联立直线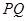 与双曲线可得
与双曲线可得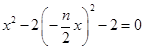
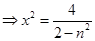 ,
,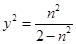 则
则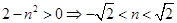 ,则
,则 ,设点
,设点 到直线
到直线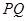 的距离为
的距离为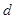 ,则
,则 到直线
到直线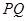 的距离也为
的距离也为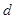 ,则
,则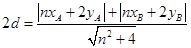 ,因为
,因为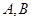 在直线
在直线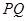 的两端,所以
的两端,所以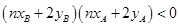 ,
,
则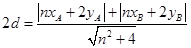

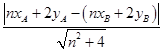 ,又因为
,又因为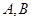 在直线
在直线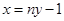 上,所以
上,所以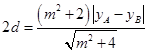
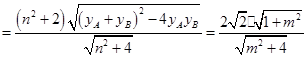 ,
,
则四边形

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:解答题
在平面直角坐标系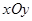 中,已知抛物线
中,已知抛物线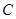 :
: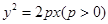 ,在此抛物线上一点
,在此抛物线上一点
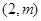 到焦点的距离是3.
到焦点的距离是3.
(1)求此抛物线的方程;
(2)抛物线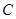 的准线与
的准线与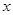 轴交于
轴交于 点,过
点,过 点斜率为
点斜率为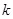 的直线
的直线 与抛物线
与抛物线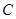 交于
交于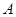 、
、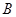 两点.是否存在这样的
两点.是否存在这样的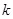 ,使得抛物线
,使得抛物线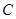 上总存在点
上总存在点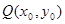 满足
满足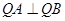 ,若存在,求
,若存在,求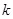 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.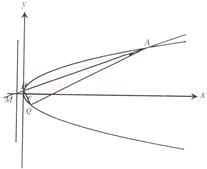
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: (
(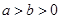 )的左焦点为
)的左焦点为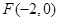 ,离心率为
,离心率为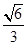 .
.
(1)求椭圆C的标准方程;
(2)设O为坐标原点,T为直线 上任意一点,过F作TF的垂线交椭圆C于点P,Q.当四边形OPTQ是平行四边形时,求四边形OPTQ的面积.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.当四边形OPTQ是平行四边形时,求四边形OPTQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,设椭圆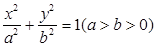 的左、右焦点分别为
的左、右焦点分别为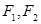 ,点
,点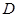 在椭圆上,
在椭圆上,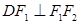 ,
,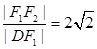 ,
,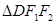 的面积为
的面积为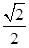 .
.
(1)求该椭圆的标准方程;
(2)设圆心在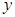 轴上的圆与椭圆在
轴上的圆与椭圆在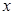 轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..
轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..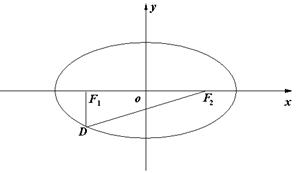
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆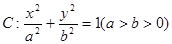 的离心率为
的离心率为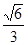 ,
,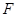 为椭圆在
为椭圆在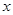 轴正半轴上的焦点,
轴正半轴上的焦点,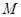 、
、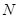 两点在椭圆
两点在椭圆 上,且
上,且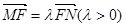 ,定点
,定点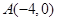 .
.
(1)求证:当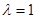 时
时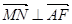 ;
;
(2)若当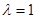 时有
时有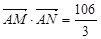 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的椭圆中,当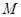 、
、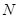 两点在椭圆
两点在椭圆 上运动时,试判断
上运动时,试判断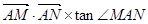 是否有最大值,若存在,求出最大值,并求出这时
是否有最大值,若存在,求出最大值,并求出这时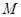 、
、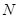 两点所在直线方程,若不存在,给出理由.
两点所在直线方程,若不存在,给出理由.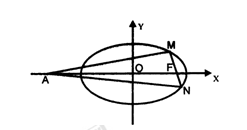
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆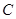 :
: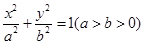 经过点
经过点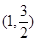 ,其离心率
,其离心率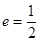 .
.
(1)求椭圆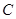 的方程;
的方程;
(2)过坐标原点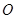 作不与坐标轴重合的直线
作不与坐标轴重合的直线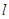 交椭圆
交椭圆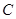 于
于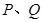 两点,过
两点,过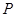 作
作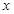 轴的垂线,垂足为
轴的垂线,垂足为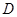 ,连接
,连接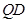 并延长交椭圆
并延长交椭圆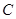 于点
于点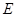 ,试判断随着
,试判断随着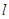 的转动,直线
的转动,直线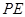 与
与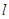 的斜率的乘积是否为定值?说明理由.
的斜率的乘积是否为定值?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆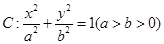 的左右焦点分别为
的左右焦点分别为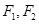 ,点
,点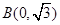 为短轴的一个端点,
为短轴的一个端点,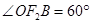 .
.
(1)求椭圆 的方程;
的方程;
(2)如图,过右焦点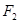 ,且斜率为
,且斜率为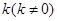 的直线
的直线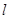 与椭圆
与椭圆 相交于
相交于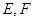 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线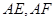 分别交直线
分别交直线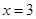 于点
于点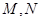 ,线段
,线段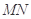 的中点为
的中点为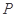 ,记直线
,记直线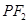 的斜率为
的斜率为 .
.
求证:  为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com