练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示的曲线图是2020年1月25日至2020年2月12日陕西省及西安市新冠肺炎累计确诊病例的曲线图，则下列判断正确的是（ ）

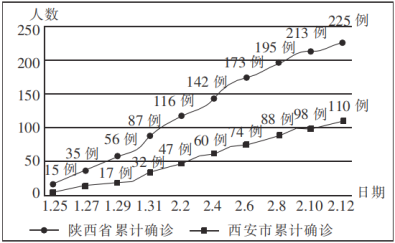
    A.1月31日陕西省新冠肺炎累计确诊病例中西安市占比超过了

    B.1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势

    C.2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了97例

    D.2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率大于2月6日到2月8日的增长率

    【答案】ABC

    【解析】

    根据曲线图可得ABC正确，2月8日到2月10日西安新冠肺炎累计确诊病例增加了，2月6日到2月8日西安新冠肺炎累计确诊病例增加了，D说法不正确.

    1月31日陕西省新冠肺炎累计确诊病例共有87例，其中西安32例，所以西安所占比例为，故A正确；

    由曲线图可知，1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势，故B正确；

    2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了例，故C正确；

    2月8日到2月10日西安新冠肺炎累计确诊病例增加了，2月6日到2月8日西安新冠肺炎累计确诊病例增加了，显然，故D错误.

    故选：ABC

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为直角梯形，其中∥，是的中点，和交于点，且平面．

    （1）证明：平面平面；

    （2）求直线与平面所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知圆锥的顶点为S，底面圆O的两条直径分别为AB和CD，且AB⊥CD，若平面平面．现有以下四个结论：

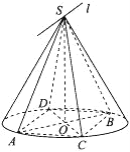
    ①AD∥平面SBC；

    ②；

    ③若E是底面圆周上的动点，则△SAE的最大面积等于△SAB的面积；

    ④与平面SCD所成的角为45°．

    其中正确结论的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若的最大值为，求的值；

    （2）若存在实数且，使得，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在极坐标系中，曲线的极坐标方程为，以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，直线的参数方程为（为参数， ）.

    （1）求曲线的直角坐标方程和直线的普通方程；

    （2）若曲线上的动点到直线的最大距离为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司A产品生产的投入成本x（单位：万元）与产品销售收入y（单位：十万元）存在较好的线性关系，下表记录了该公司最近8次该产品的相关数据，且根据这8组数据计算得到y关于x的线性回归方程为．

    x（万元）

    6

    7

    8

    11

    12

    14

    17

    21

    y（十万元）

    1.2

    1.5

    1.7

    2

    2.2

    2.4

    2.6

    2.9

    （1）求的值（结果精确到0.0001），并估计公司A产品投入成本30万元后产品的销售收入（单位：十万元）．

    （2）该公司B产品生产的投入成本u（单位：万元）与产品销售收入v（单位：十万元）也存在较好的线性关系，且v关于u的线性回归方程为．

    （i）估计该公司B产品投入成本30万元后的毛利率（毛利率）；

    （ii）判断该公司A，B两个产品都投入成本30万元后，哪个产品的毛利率更大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）则下列结论错误的是（ ）

    A.函数f（x）的值域为RB.函数f（|x|）为偶函数

    C.函数f（x）为奇函数D.函数f（x）是定义域上的单调函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点 ，且离心率为.设为椭圆的左、右顶点，P为椭圆上异于的一点，直线分别与直线相交于两点，且直线与椭圆交于另一点.

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）求证：直线与的斜率之积为定值；

    （Ⅲ）判断三点是否共线，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    (1)求函数的极值；

    (2)设，对于任意，总有成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案