
【题目】函数 ![]() 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
【答案】C
【解析】解:由已知 ![]() ,则ω=2
,则ω=2
f(x)=sin(2x+φ)向左移 ![]() 个单位得
个单位得 ![]() 为奇函数
为奇函数
则有 ![]() ,
,
∵|φ|< ![]() ∴φ=
∴φ= ![]()
即 ![]() .代入选项检验,当x=
.代入选项检验,当x= ![]() 时,
时, ![]() 为函数的最大值
为函数的最大值
根据三角函数的性质可知对称轴处将取得函数的最值,C正确.
故选:C
【考点精析】本题主要考查了正弦函数的对称性和函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() ;图象上所有点向左(右)平移
;图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1-![]() 时,切线MA的斜率为-
时,切线MA的斜率为-![]() .
.
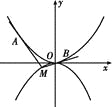
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三学生中随机抽取了![]() 名学生,统计了期末数学考试成绩如下表:
名学生,统计了期末数学考试成绩如下表:
(1)请在频率分布表中的①、②位置上填上相应的数据,并在给定的坐标系中作出这些数据的频率分布直方图,再根据频率分布直方图估计这![]() 名学生的平均成绩;
名学生的平均成绩;
(2)用分层抽样的方法在分数在![]() 内的学生中抽取一个容量为
内的学生中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取![]() 人,求至少有
人,求至少有![]() 人的分数在
人的分数在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段上![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角
![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里, ![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位
(单位![]() )的情况如下表1:
)的情况如下表1:
![]()
哈尔滨市某月![]() 指数频数分布如下表2:
指数频数分布如下表2:
![]()
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(参考公式: ![]() ,其中
,其中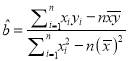 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当![]() 不高于200时,洗车店平均每天亏损约2000元;当
不高于200时,洗车店平均每天亏损约2000元;当![]() 在
在![]() 时,洗车店平均每天收入约4000元;当
时,洗车店平均每天收入约4000元;当![]() 大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
大于400时,洗车店平均每天收入约7000元;根据表2估计校长的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),函数f(x)=
=(1,sin2x),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(1)当x= ![]() 时,求|a﹣b|的值;
时,求|a﹣b|的值;
(2)求函数f(x)的最小正周期以及单调递增区间;
(3)求方程f(x)=k,(0<k<2),在[﹣ ![]() ,
, ![]() ]内的所有实数根之和.
]内的所有实数根之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有两个面平行,其余各面都是四边形的几何体叫棱柱.
B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱.
C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥.
D.棱台各侧棱的延长线交于一点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com