
【题目】某单位附近只有甲,乙两个临时停车场,它们各有50个车位,为了方便市民停车,某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录,如下表:
时间 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
停车场甲 | 10 | 3 | 12 | 6 | 12 | 17 |
停车场乙 | 13 | 4 | 3 | 2 | 6 | 19 |
如果表中某一时刻停车场剩余停车位数低于总车位数的10%,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(Ⅰ)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(Ⅱ)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(Ⅲ)当停车场乙发出饱和警报时,求停车场甲也发出饱和警报的概率.
【答案】解:(Ⅰ)事件“该车主收到停车场甲饱和警报”只有10点这一种情况,
该车主抵达单位共有六种情况,
所以该车主收到停车场甲饱和警报的概率为 ![]() .
.
(Ⅱ)事件“甲停车场比乙停车场剩余车位数少”有8点、10点、18点三种情况,
一共有六个时刻,
所以甲停车场比乙停车场剩余车位数少的概率为 ![]() .
.
(Ⅲ)事件“停车场乙发出饱和警报”有10点、12点、14点三种情况,
事件“停车场甲也发出饱和警报”只有10点一种情况,
所以当停车场乙发出饱和警报时,
停车场甲也发出饱和警报的概率为 ![]()
【解析】(Ⅰ)事件“该车主收到停车场甲饱和警报”只有10点这一种情况,该车主抵达单位共有六种情况,由此能求出该车主收到停车场甲饱和警报的概率.(Ⅱ)事件“甲停车场比乙停车场剩余车位数少”有8点、10点、18点三种情况,一共有六个时刻,由此能求出甲停车场比乙停车场剩余车位数少的概率.(Ⅲ)事件“停车场乙发出饱和警报”有10点、12点、14点三种情况,事件“停车场甲也发出饱和警报”只有10点一种情况,由此能求出当停车场乙发出饱和警报时,停车场甲也发出饱和警报的概率.


科目:高中数学 来源: 题型:
【题目】已知甲、乙两个容器,甲容器容量为x,装满纯酒精,乙容器容量为z,其中装有体积为y的水(x,y<z,单位:L).现将甲容器中的液体倒入乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒入甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过n(n∈N*)次操作之后,乙容器中含有纯酒精an(单位:L),下列关于数,列{an}的说法正确的是( )
A.当x=y=a时,数列{an}有最大值 ![]()
B.设bn=an+1﹣an(n∈N*),则数列{bn}为递减数列
C.对任意的n∈N* , 始终有 ![]()
D.对任意的n∈N* , 都有 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程![]() 的有一个正实根,一个负实根,
的有一个正实根,一个负实根,![]() ;
;
③![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]() 时,
时,![]()
④函数![]() 的值域是
的值域是![]() .
.
其中正确命题的序号是_____(把所有正确命题的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为非负整数的数列{an}同时满足下列条件: ①a1=m(m∈N*);②an≤n﹣1(n≥2);③n是a1+a2+…+an的因数(n≥1).
(Ⅰ)当m=5时,写出数列{an}的前五项;
(Ⅱ)若数列{an}的前三项互不相等,且n≥3时,an为常数,求m的值;
(Ⅲ)求证:对任意正整数m,存在正整数M,使得n≥M时,an为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0,|φ|≤ ![]() )的部分图象如图所示,若方程f(x)=a在x∈[﹣
)的部分图象如图所示,若方程f(x)=a在x∈[﹣ ![]() ,
, ![]() ]上有两个不相等的实数根,则a的取值范围是( )
]上有两个不相等的实数根,则a的取值范围是( ) 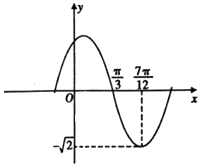
A.[ ![]() ,
, ![]() )
)
B.[﹣ ![]() ,
, ![]() )
)
C.[﹣ ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( ) 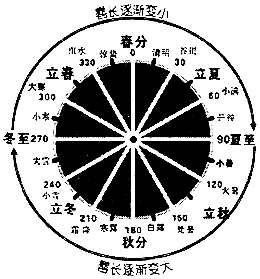
A.五寸
B.二尺五寸
C.三尺五寸
D.四尺五寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com