练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知非零向量列满足：，，（，）.

    （1）证明：数列是等比数列；

    （2）向量与的夹角；

    （3）设，将中所有与共线的向量按原来的顺序排成一列，记作，令，为坐标原点，求点的坐标.

    【答案】（1）证明见解析；（2）；（3）.

    【解析】

    （1）由已知得，可得，从而，由此可证明；

    （2）设与的夹角为，，

    结合代换得，由向量夹角公式即可求解；

    （3）由（2）知相邻两向量夹角为，每相隔三个向量的两向量必定共线并方向相反，即，设，由（1）可求得，由此求出

    （1）由已知得，

    ，，

    是以为首项，为公比的等比数列；

    （2）设与的夹角为，

    ，

    ，，即与的夹角为；

    （3）由（2）知相邻两向量的夹角为，每相隔三个向量的两向量必定共线并方向相反，即，设，由（1）知，，

    ，

    结合等比数列前项和公式可得

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了对某课题进行研究，用分层抽样方法从三所高校A,B,C的相关人员中，抽取若干人组成研究小组、有关数据见下表（单位：人）

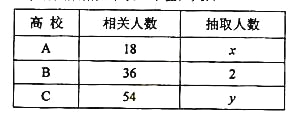
    （I） 求x,y ;

    （II） 若从高校B、C抽取的人中选2人作专题发言，求这二人都来自高校C的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，其中是自然对数的底数，.

    （1）当时，证明：；

    （2）是否存在实数，使的最小值为3，如果存在，求出的值；如果不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了迎接2019年全国文明城市评比，某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会，通过随机抽样，得到参加问卷调查的1000人的得分（满分：100分）数据，统计结果如下表所示：

    组别

    频数

    25

    150

    200

    250

    225

    100

    50

    （1）由频数分布表可以认为，此次问卷调查的得分服从正态分布，近似为这1000人得分的平均值（同一组数据用该组区间的中点值作为代表），请利用正态分布的知识求；

    （2）在（1）的条件下，文明办为此次参加问卷调查的市民制定如下奖励方案：

    （i）得分不低于的可以获赠2次随机话费，得分低于的可以获赠1次随机话费；

    （ii）每次获赠的随机话费和对应的概率为：

    获赠的随机话费（单位：元）

    20

    40

    概率

    现市民小王要参加此次问卷调查，记（单位：元）为该市民参加问卷调查获赠的话费，求的分布列及数学期望.

    附：①；

    ②若，则，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂销售部以箱为单位销售某种零件，每箱的定价为元，低于箱按原价销售，不低于箱则有以下两种优惠方案：①以箱为基准，每多箱送箱；②通过双方议价，买方能以优惠成交的概率为，以优惠成交的概率为.

    甲、乙两单位都要在该厂购买箱这种零件，两单位都选择方案②，且各自达成的成交价格相互独立，求甲单位优惠比例不低于乙单位优惠比例的概率；

    某单位需要这种零件箱，以购买总价的数学期望为决策依据，试问该单位选择哪种优惠方案更划算？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂销售部以箱为单位销售某种零件，每箱的定价为元，低于箱按原价销售，不低于箱则有以下两种优惠方案：①以箱为基准，每多箱送箱；②通过双方议价，买方能以优惠成交的概率为，以优惠成交的概率为.

    甲、乙两单位都要在该厂购买箱这种零件，两单位都选择方案②，且各自达成的成交价格相互独立，求甲单位优惠比例不低于乙单位优惠比例的概率；

    某单位需要这种零件箱，以购买总价的数学期望为决策依据，试问该单位选择哪种优惠方案更划算？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求适合下列条件的椭圆的标准方程：

    （1）长轴长是10，离心率是；

    （2）在x轴上的一个焦点，与短轴两个端点的连线互相垂直，且焦距为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年世界服装市场是富有经济活力的一年，某国有企业为了使2019年服装效益更上一层楼，决定进一步深化企业改革、制定好的政策，为此，该企业对某品牌服装2018年1月份~5月份的销售量（万件）与利润（万元）作统计数据如下表：

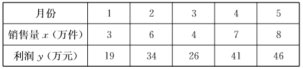
    （1）从这个月的利润（单位：万元）中任选个月，求此个月利润均大于万元且小于万元的概率；

    （2）已知销售量（万件）与利润（万元）大致满足线性相关关系，请根据前个月的数据，求出关于的线性回归方程；

    （3）若由线性回归方程得到的利润的估计数据与真实数据的误差不超过万元，则认为得到的利润的估计数据是理想的.请用表格中第个月的数据检验由（2）中回归方程所得的第个月的利润的估计数据是否理想.

    注：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在多面体中, 平面,,四边形是边长为的菱形.

    （1）证明: ；

    （2）线段上是否存在点,使平面,若存在,求的值；若不存在,请说明理由.

    查看答案和解析>>

    同步练习册答案