
函数 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数 ,在定义域中存在
,在定义域中存在 使
使 ,
, ,且满足以下3个条件。
,且满足以下3个条件。
(1) 是
是 定义域中的数,
定义域中的数, ,则
,则
(2) ,(
,( 是一个正的常数)
是一个正的常数)
(3)当 时,
时, 。
。
证明:(1) 是奇函数;
是奇函数;
(2) 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3) 在
在 内为减函数。
内为减函数。
科目:高中数学 来源: 题型:
| f(x1)f(x2)+1 | f(x2)-f(x1) |
查看答案和解析>>
科目:高中数学 来源:设计必修一数学(人教A版) 人教A版 题型:022
由于任意x和-x均要在定义域内,故奇函数或偶函数的定义域一定关于________对称.所以,我们在判定函数的奇偶性时,首先要确定函数的定义域(函数的定义域关于原点对称是函数具有奇偶性的必要条件.如果其定义域关于原点不对称,那么它没有奇偶性).然后再判断________与________的关系,从而确定其奇偶性.
查看答案和解析>>
科目:高中数学 来源:2015届河南省高一第一次阶段数学试卷(奥赛班)(解析版) 题型:解答题
已知函数 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①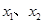 、
、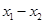 是定义域中的数时,有
是定义域中的数时,有 ;
;
②
 是定义域中的一个数);
是定义域中的一个数);
③当 时,
时, .
.
(1)判断 与
与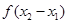 之间的关系,并推断函数
之间的关系,并推断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在 上的单调性,并证明;
上的单调性,并证明;
(3)当函数 的定义域为
的定义域为 时,
时,
①求 的值;②求不等式
的值;②求不等式 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源:2014届北京师大附中高一上学期期末考试数学试卷 题型:解答题
函数 的定义域关于原点对称,但不包括数0,对定义域中的任意实数
的定义域关于原点对称,但不包括数0,对定义域中的任意实数 ,在定义域中存在
,在定义域中存在 使
使 ,
, ,且满足以下3个条件。
,且满足以下3个条件。
(1) 是
是 定义域中的数,
定义域中的数, ,则
,则
(2) ,(
,( 是一个正的常数)
是一个正的常数)
(3)当 时,
时, 。
。
证明:(1) 是奇函数;
是奇函数;
(2) 是周期函数,并求出其周期;
是周期函数,并求出其周期;
(3) 在
在 内为减函数。
内为减函数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com