
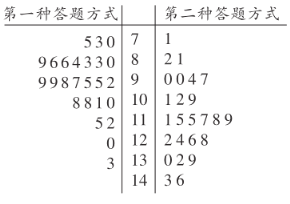
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФКазгжазАга4ИіДѓаЁЁЂаЮзДЁЂЪжИаЭъШЋЯрЭЌЕФаЁЧђЃЌЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЎЯжУПДЮгаЗХЛиЕиДгжаШЮвтШЁГівЛИіаЁЧђЃЌжБЕНБъгаХМЪ§ЕФЧђЖМШЁЕНЙ§ОЭЭЃжЙЃЎаЁУїгУЫцЛњФЃФтЕФЗНЗЈЙРМЦЧЁКУдкЕк4ДЮЭЃжЙУўЧђЕФИХТЪЃЌРћгУМЦЫуЛњШэМўВњЩњЫцЛњЪ§ЃЌУП1зщжага4ИіЪ§зжЃЌЗжБ№БэЪОУПДЮУўЧђЕФНсЙћЃЌОЫцЛњФЃФтВњЩњСЫвдЯТ21зщЫцЛњЪ§ЃКгЩДЫПЩвдЙРМЦЧЁКУдкЕк4ДЮЭЃжЙУўЧђЕФИХТЪЮЊЃЈ ЃЉ
1314 1234 2333 1224 3322 1413 3124 4321 2341 2413 1224 2143 4312
2412 1413 4331 2234 4422 3241 4331 4234
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 ЯАЬтОЋбЁЯЕСаД№АИ
ЯАЬтОЋбЁЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЪЕбщжабЇЪ§бЇНЬбазщЃЌдкИпШ§РэПЦвЛАрНјааСЫвЛДЮЁАВЩгУСНжжВЛЭЌЗНЪННјааД№ОэЁБЕФПМЪдЪЕбщЃЌЕквЛжжзіОэЗНЪНЃКАДДгЧАЭљКѓЕФЫГађвРДЮзіЃЛЕкЖўжжзіОэЗНЪНЃКЯШзіМђЕЅЬтЃЌдйзіФбЬт.ЮЊСЫБШНЯетСНжжзіОэЗНЪНЕФаЇТЪЃЌбЁШЁСЫ![]() УћбЇЩњЃЌНЋЫћУЧЫцЛњЗжГЩСНзщЃЌУПзщ
УћбЇЩњЃЌНЋЫћУЧЫцЛњЗжГЩСНзщЃЌУПзщ![]() ШЫ.ЕквЛзщбЇЩњгУЕквЛжжЗНЪНЃЌЕкЖўзщбЇЩњгУЕкЖўжжЗНЪНЃЌИљОнбЇЩњЕФПМЪдЗжЪ§ЃЈЕЅЮЛЃКЗжЃЉЛцжЦСЫОЅвЖЭМШчЭМЫљЪО.
ШЫ.ЕквЛзщбЇЩњгУЕквЛжжЗНЪНЃЌЕкЖўзщбЇЩњгУЕкЖўжжЗНЪНЃЌИљОнбЇЩњЕФПМЪдЗжЪ§ЃЈЕЅЮЛЃКЗжЃЉЛцжЦСЫОЅвЖЭМШчЭМЫљЪО.
![]() Шє
Шє![]() ЗжЃЈКЌ
ЗжЃЈКЌ![]() ЗжЃЉвдЩЯЮЊгХауЃЌИљОнОЅвЖЭМЙРМЦСНжжзіОэЗНЪНЕФгХауТЪЃЛ
ЗжЃЉвдЩЯЮЊгХауЃЌИљОнОЅвЖЭМЙРМЦСНжжзіОэЗНЪНЕФгХауТЪЃЛ
![]() Щш
Щш![]() УћбЇЩњПМЪдЗжЪ§ЕФжаЮЛЪ§ЮЊ
УћбЇЩњПМЪдЗжЪ§ЕФжаЮЛЪ§ЮЊ![]() ЃЌИљОнОЅвЖЭМЬюаДЯТУцЕФ
ЃЌИљОнОЅвЖЭМЬюаДЯТУцЕФ![]() СаСЊБэЃК
СаСЊБэЃК
ГЌЙ§жаЮЛЪ§ | ВЛГЌЙ§жаЮЛЪ§ | КЯМЦ | |
ЕквЛжжзіОэЗНЪН | |||
ЕквЛжжзіОэЗНЪН | |||
КЯМЦ |
ИљОнСаСЊБэЃЌФмЗёга![]() ЕФАбЮеШЯЮЊСНжжзіОэЗНЪНЕФаЇТЪгаВювьЃП
ЕФАбЮеШЯЮЊСНжжзіОэЗНЪНЕФаЇТЪгаВювьЃП
ИНЃК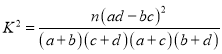 ЃЌ
ЃЌ![]() .
.
|
|
|
|
|
|
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЖдгкКЏЪ§
ЃЌЖдгкКЏЪ§![]() гаЯТЪіЫФИіНсТлЃК
гаЯТЪіЫФИіНсТлЃК
ЂйКЏЪ§![]() дкЦфЖЈвхгђЩЯЮЊдіКЏЪ§ЃЛ
дкЦфЖЈвхгђЩЯЮЊдіКЏЪ§ЃЛ
ЂкЖдгкШЮвтЕФ![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЛ
ГЩСЂЃЛ
Ђл![]() гаЧвНігаСНИіСуЕуЃЛ
гаЧвНігаСНИіСуЕуЃЛ
ЂмШє![]() дкЕу
дкЕу![]() ДІЕФЧаЯпвВЪЧ
ДІЕФЧаЯпвВЪЧ![]() ЕФЧаЯпЃЌдђ
ЕФЧаЯпЃЌдђ![]() БиЪЧ
БиЪЧ![]() СуЕуЃЎ
СуЕуЃЎ
ЦфжаЫљгае§ШЗЕФНсТлађКХЪЧЃЈ ЃЉ
A.ЂйЂкЂлB.ЂйЂкC.ЂкЂлЂмD.ЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпyЃНaЗжБ№гыжБЯп![]() ЃЌЧњЯп
ЃЌЧњЯп![]() НЛгкЕуAЃЌBЃЌдђЯпЖЮABГЄЖШЕФзюаЁжЕЮЊ______ЃЎ
НЛгкЕуAЃЌBЃЌдђЯпЖЮABГЄЖШЕФзюаЁжЕЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтжљABCЉA1B1C1жаЃЌABЁЭВрУцBCC1B1ЃЌACЃНAB1ЃЎ
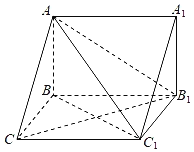
ЃЈ1ЃЉЧѓжЄЃКЦНУцABC1ЁЭЦНУцAB1CЃЛ
ЃЈ2ЃЉШєABЃНBCЃН2ЃЌЁЯBCC1ЃН60ЁуЃЌЧѓЖўУцНЧBЉAC1ЉB1ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЁїABCБпГЄЮЊ3ЃЌЕуMЃЌNЗжБ№ЪЧABЃЌACБпЩЯЕФЕуЃЌANЃНBMЃН1ЃЌШчЭМ1ЫљЪОЃЎНЋЁїAMNбиMNелЦ№ЕНЁїPMNЕФЮЛжУЃЌЪЙЯпЖЮPCГЄЮЊ![]() ЃЌСЌНгPBЃЌШчЭМ2ЫљЪОЃЎ
ЃЌСЌНгPBЃЌШчЭМ2ЫљЪОЃЎ
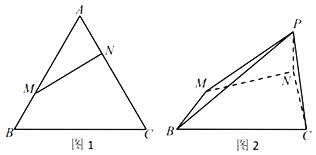
ЃЈЂёЃЉЧѓжЄЃКЦНУцPMNЁЭЦНУцBCNMЃЛ
ЃЈЂђЃЉШєЕуDдкЯпЖЮBCЩЯЃЌЧвBDЃН2DCЃЌЧѓЖўУцНЧMЉPDЉCЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
(1)Шє![]() жЛга
жЛга![]() Иіе§ећЪ§НтЃЌЧѓ
Иіе§ећЪ§НтЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
(2)ЂйЧѓжЄЃКЗНГЬ![]() гаЮЈвЛЪЕИљ
гаЮЈвЛЪЕИљ![]() ЃЌЧв
ЃЌЧв![]() ЃЛ
ЃЛ
ЂкЧѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌгжКЏЪ§
ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌгжКЏЪ§![]() .
.
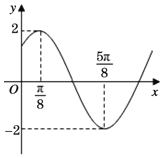
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїдіЧјМфЃЛ
ЕФЕЅЕїдіЧјМфЃЛ
ЃЈ2ЃЉЩш![]() ЕФФкНЧ
ЕФФкНЧ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФЖдБпЗжБ№ЮЊ
ЕФЖдБпЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌгж
ЃЌгж![]() ЃЌЧвШёНЧ
ЃЌЧвШёНЧ![]() Тњзу
Тњзу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЃЌЧѓ
БпЕФжаЕуЃЌЧѓ![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЕуMЪЧРтГЄЮЊ2ЕФе§ЗНЬхABCD-A1B1C1D1ЕФРтADЕФжаЕуЃЌЕуPдкУцBCC1B1ЫљдкЕФЦНУцФкЃЌШєЦНУцD1PMЗжБ№гыЦНУцABCDКЭЦНУцBCC1B1ЫљГЩЕФШёЖўУцНЧЯрЕШЃЌдђЕуPЕНЕуC1ЕФзюЖЬОрРыЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.1D.
C.1D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com