
����Ŀ��ij���ֵĻ�������Ϊ![]() ����λ��Ԫ��������������շ��ֵ�Ͷ���˳�Ϊ�����ˣ������˵ı���ȵı��������ϴ��ȵij��մ����Ĺ������£�
����λ��Ԫ��������������շ��ֵ�Ͷ���˳�Ϊ�����ˣ������˵ı���ȵı��������ϴ��ȵij��մ����Ĺ������£�

�������һ������һ���ڳ��մ�������Ӧ�������£�

(1) ��һ�����˱���ȵı��Ѹ��ڻ������ѵĸ��ʣ�
(2) ��һ�����˱���ȵı��Ѹ��ڻ��������ã����䱣�ѱȻ������Ѹ߳�60%�ĸ��ʣ�
(3) �������˱���ȵ�ƽ��������������ѵı�ֵ.
���𰸡�(1)0.55��(2) ![]() ��(3)1.23.
��(3)1.23.
�����������������
(1)���ø��ʵ����ʿɵ�һ�����˱���ȵı��Ѹ��ڻ������ѵĸ�����0.55��
(2)����������ʼ��㹫ʽ�ɵ�һ�����˱���ȵı��Ѹ��ڻ��������ã����䱣�ѱȻ������Ѹ߳�60%�ĸ�����![]() ��
��
(3)�����г��ֲ��У�Ȼ���Ϸֲ��м���ɵ������˱���ȵ�ƽ��������������ѵı�ֵ��1.23.
���������
(1) ��![]() ��ʾ�¼�����һ�����˱���ȵı��Ѹ��ڻ������ѡ������¼�
��ʾ�¼�����һ�����˱���ȵı��Ѹ��ڻ������ѡ������¼�![]() �������ҽ���һ���ڳ��մ�������1����
�������ҽ���һ���ڳ��մ�������1����![]()
(2) ��![]() ��ʾ�¼�����һ�����˱���ȵı��ѱȻ������Ѹ߳�60%�������¼�
��ʾ�¼�����һ�����˱���ȵı��ѱȻ������Ѹ߳�60%�������¼�![]() �������ҽ���һ���ڳ��մ�������3����
�������ҽ���һ���ڳ��մ�������3����![]()
��![]() ����
����![]() ���������ĸ���Ϊ
���������ĸ���Ϊ![]()
(3)�������˱���ȵı���Ϊ![]() ����
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
| 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
![]() ����������˱���ȵ�ƽ��������������ѵı�ֵΪ
����������˱���ȵ�ƽ��������������ѵı�ֵΪ![]()


 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1����![]() ��֤����
��֤���� ![]() ��
��![]() �ϴ���Ψһ��㣻
�ϴ���Ψһ��㣻
��2���躯��![]() ����
���� ![]() ��ʾ
��ʾ![]() �еĽ�Сֵ������
�еĽ�Сֵ������![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=xlnx��g��x��=��x2+ax��3��
��1������f��x����[t��t+2]��t��0���ϵ���Сֵ��
��2����һ��x�ʣ�0��+�ޣ���2f��x����g��x�����������ʵ��a��ȡֵ��Χ��
��3��֤������һ��x�ʣ�0��+�ޣ�������lnx�� ![]() ��
�� ![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������Բ�ķ���
��1�������� ![]() ����Բ����y���ϵ�Բ�ķ��̣�
����Բ����y���ϵ�Բ�ķ��̣�
��2��Բ�ĵİ뾶Ϊ1��Բ����㣨1��0������ ![]() �ԳƵ�Բ�ķ���.
�ԳƵ�Բ�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��B�ֱ���ֱ��l1��x��y��7��0��l2��x��y��5��0���ƶ�����AB���е�M��ԭ��ľ������СֵΪ( )
A.3 ![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
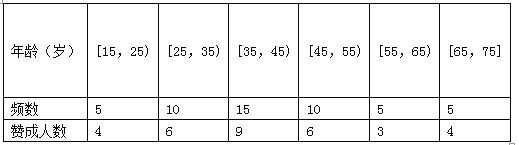
����Ŀ��˽�ҳ���β���ŷ������������������Ҫ����֮һ�����������������Ӧ���ᳫ��̼����ٿ�˽�ҳ�������ѡ����ɫ���з�ʽ��ΪԤ��������һ������Ϊ�ˣ��ܶ����ʵʩ�˻�������β�����У�����ij����Ϊ�˽��������ڶ���������������̬�ȣ���������50�ˣ���������������������Ƴ��±���
��������ɱ�������Ա��Ƶ�ʷֲ�ֱ��ͼ��
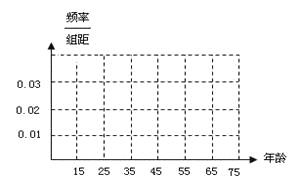
����������������[15��25����[25��35���ı��������и����ѡȡ2�˽����ٵ��飬��ǡ��2�˲��ɵĸ��ʣ�
�������ڣ������������£��ټ�ѡ�е�4���в���������������������Ϊ![]() �����������
�����������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�����M���� ![]() ��
�� ![]() ����N��
����N�� ![]() ����
���� ![]() ����ֱ�ߴ�ֱ����ֱ��l����б���ǣ� ����
����ֱ�ߴ�ֱ����ֱ��l����б���ǣ� ����
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����߷���Ϊx2=2py��p��0�����佹��ΪF����OΪ����ԭ�㣬������F��б��Ϊk��k��0����ֱ���������߽���A��B���㣬��A��B����ֱ��������ߵ��������ߣ����������߽��ڵ�M��
��1���� ![]() ��
��
��2����ֱ��MF�������߽���C��D���㣬���ı���ACBD�����Ϊ ![]() ����ֱ��AB��б��k��
����ֱ��AB��б��k��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() ��
�� ![]() ��������Ϊ
��������Ϊ![]() ��
�� ![]() Ϊ��Բ
Ϊ��Բ![]() ���ҽ��㣬
���ҽ��㣬 ![]() ��
�� ![]() .
.
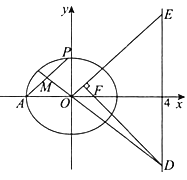
��������Բ![]() �ķ��̣�
�ķ��̣�
������![]() Ϊԭ�㣬
Ϊԭ�㣬 ![]() Ϊ��Բ��һ�㣬
Ϊ��Բ��һ�㣬 ![]() ���е�Ϊ
���е�Ϊ![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ����֤��
����֤�� ![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com