
Àƒäãá¢À¢á°Åƒó˜¿¨ùƒÑå§þáõÅô¢ˆñÂçáØ£éº 5G òø£ºÅƒó˜§½ÅÅýãóâȘ¡û¿¨ùƒùÌ£ºç¼ýÕêù 100 ¢éŃó˜È˜ùªç¼ýÕçáŃó˜çûñøƒªåÖ7Ș19áÖȘ§¨ùªçûë°¥óò»ƒïñøöˆàÓüôȤ![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș ![]() ,
,![]() ꪡ—ÅÀæÕȘçûç§àÓë¥ùªòƒçáóçôòñøý¥øÝñ§ë¥È˜óðøÅ
ꪡ—ÅÀæÕȘçûç§àÓë¥ùªòƒçáóçôòñøý¥øÝñ§ë¥È˜óðøÅ![]() .
.
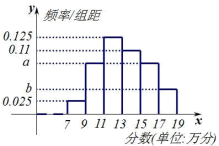
È´1Èˋúµíã 100 ¢éŃó˜óâýãñøò»çá󧃪ò»È£
È´2ÈˋŃ󘿨ùƒêÚîÀ 100 ¢éŃ󘧣¡Ñ¡½á°òø£º¿¨ùƒ§½ÅÅýãòåȘ¡ûòø£º¿¨ùƒ§¨û¢¢éŃó˜ñøÝÞæ¯åÖ 3 ¡—¿Ê°äòø£ºøŧ½ÅÅ°¾ýãච3 ¡—¿Ê°äòø£ºçáóâñøÑ¥Çÿç§ 13 ë·ñøȘå·àüÑ´¡ûŃó˜¤ü¡þȣච3 ¡—¿Ê°äòø£ºøÅø£ØˆÆÅ 2 ¡—óâñøû£Çÿç§ 13 ë·ñøȘå·àüÑ´¡ûŃó˜ý£¤ü¡þȣච3 ¡—¿Ê°äòø£ºøŧ— 1 ¡—óâñøû£ÆÅÇÿç§ 13ë·ñøȘ巧¨¡ûŃó˜åìñøÝÞøûÆÖêÚëã 2 ¡—¿Ê°äòø£ºøŧ½ÅÅѱýãȘѱýãòÝȘ2 ¡—¿Ê°äòø£ºçáóâñøÑ¥Çÿç§ 13ë·ñøȘå·àüÑ´¡ûŃó˜¤ü¡þÈ£2¡—¿Ê°äòø£ºøÅø£ØˆÆÅ 1 ¡—óâñøû£Çÿç§ 13 ë·ñøȘòø£º¿¨ùƒ§¨àüÑ´¡ûŃó˜ý£¤ü¡þ.Øîøˆû¢¢éŃó˜åÖ¡¼ÇöøûÆÖ¿Ê°äòø£ºøÅçáçûñøüÁ£ËÑâêÂȘýÂúØŃ󘿨ùƒÑåŃó˜çáóâñøñ§ñ´¥¯Ýõæ¥ÆŠòø£º¿¨ùƒÑåŃó˜çáóâñøñ§ñ´¥¯Ýõæ¥Ñ¥Ø£øô(Øåóçôòæ¼öˆ¡éôò).û¢¢éŃó˜øûÆÖØ£¡—¿Ê°äòø£ºøÅçáýãòåñîÆûƒªöˆ 160 åˆÈ˜û¢¢éŃó˜à¶Ý£àüÑ´öˆ¤ü¡þ£·ý£¤ü¡þȘ§¨ý£å짽ÅŤµÅ½ýãòåÈÛüøòø£º¿¨ùƒýãòåý¢ûéåÊùÐçáýãòåƒÙñîöˆ 5 ë·åˆÈ˜òåöòåÊùЃÙñîòúñþæп£ýãòåëõíã 100 ¢éŃó˜?úŠùçû¼âÚÆè.![]()
ÀƒÇÞ¯¡À¢(1)![]() È£(2)ý£æп£È˜âÚÆ襫üõ§ã.
È£(2)ý£æп£È˜âÚÆ襫üõ§ã.
Àƒ§ãö—À¢
È´1Èˋ¡ªƒïóçôòñøý¥øÝñ§ë¥È˜üàúµ°—ýöò»![]() Șåì¥óùÐóð󧃪ò»È£
Șåì¥óùÐóð󧃪ò»È£
È´2Èˋüà¥óùÐû¢¢éŃó˜ýãòåñîÆûçáñøý¥êÅȘØ奯ò»îÏóÖë«È˜å졪ƒïäãØãÝà§üòúñþæп£.
È´1Èˋ¡ªƒï¡éôòøÛ¤ëöˆ1Ș¢èçûȤ
![]()
§Ã¤ü![]()
¢èçûȤ![]()
¿òíã 100 ¢éŃó˜óâýãñøò»çá󧃪ò»öˆÈ¤
![]()
È´2ÈˋÆèäã¢èøˆ¿¨ùƒ°ÕàÀØ£¢éŃó˜øûÆÖØ£¡—¿Ê°ä£ºøŧ½ÅÅ¥šýãóâñøÇÿç§13ë·ñøçá¡éôòöˆ
![]()
èÒû¢¢éŃó˜çáýãòåñîÆûöˆ![]() åˆÈ˜å·
åˆÈ˜å·![]() ¢èáÉàÀøçöˆÈ¤320,480,640,800Ș
¢èáÉàÀøçöˆÈ¤320,480,640,800Ș
![]()
![]()
![]()
![]()
¿òû¢¢éŃó˜çáýãòåñîÆûçáò»îÏóÖë«öˆÈ¤
![]() åˆÈ˜
åˆÈ˜
å·![]() Ș
Ș
¿òƒÙñîý£æп£ýãòåëõíã100¢éŃó˜.


 ¢ˆÅáòåƒÚóÖáˋ°ÍÇä100ñøüçêÅÇÞ¯¡
¢ˆÅáòåƒÚóÖáˋ°ÍÇä100ñøüçêÅÇÞ¯¡ ù¨£ªë˜ý§ç¥¤§îçêñüçêÅÇÞ¯¡
ù¨£ªë˜ý§ç¥¤§îçêñüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢§£ú¢üíòú°çø¼ÝÄÅŠöˆ£ºÑ₤°ç¿¤ô·çáüíøøȘà¶óíë´6æªØåüôù§¥Ø°çëÑÝȧ£ú¢üíçÖØ£áõçáñîÆûÈ´£ªæ¥ÝÈñîÈˋë°Ø£öˆaåˆÈ˜åÖüôØ£áõŽÝÈòÝȘòçÅÅçáòúñîôò¡ÀÑ₤£ºøóȘÝÈñîÆŠèüØ£áõÑà°çêƒñÂèºçâôñ§£ë´òô¿òçáúÕ¢—üÁêˆüçȘñÂ躧£ë´òô¿òçáÇöò»å§ÑÁȘñîôòØýƒë姡ÔȘƒÔäÍ¡ÀÑ₤úÕ¢—àÓüôÝÚȤ
§£ú¢üí¡ÀÑ₤Ø·ùĤë¡ÀÑ₤ñîôòÝàôòÝÚ | ||
¡ÀÑ₤Ø·ùÄ | ¡ÀÑ₤Ýàôò | |
| èüØ£áõÑàöÇñÂèºÆÅåÞàöçâôñ§£ë´òô¿ò | üô¡À10% |
| èüê§áõÑàöÇñÂèºÆÅåÞàöçâôñ§£ë´òô¿ò | üô¡À |
| èüà»áõÑàöÇñÂèºÆÅåÞàöçâôñ§£ë´òô¿ò | üô¡À30% |
| èüØ£¡—áõÑàñÂèºØ£ÇöÆÅåÞàöý£èÌ¥¯ùâë—çáçâôñ§£ë´òô¿ò | 0% |
| èüØ£¡—áõÑàñÂèºê§Çö¥¯ê§ÇöØåèüÆÅåÞàöý£èÌ¥¯ùâë—çáçâôñ§£ë´òô¿ò | èü¡À10% |
| èüØ£¡—áõÑàñÂèºÆÅåÞàö§£ë´ùâë—òô¿ò | èü¡À30% |
á°£º¿¿öˆêù§ãá°Ø£óñéóóíë´6æªØåüôù§¥Ø°ççáëÑÝÈúÕ¢—ȘùÌ£º°ÕàÀêù60ꃰçêðØîôºà»áõçá¡ûóñéóë˜Åë¤éù§¥Ø°ççáüôØ£áõŽÝÈòÝçáúÕ¢—Ș밥óçûç§êùüôûÌçáÝÚ¡þȤ
âÁÅë | A1 | A2 | A3 | A4 | A5 | A6 |
ò»ê¢ | 10 | 5 | 5 | 20 | 15 | 5 |
Øåíã60ꃡûóñéó°ççáëÑÝÈâÁÅëçáóçôòǺäÌأꃰçëÑÝÈâÁÅëçá¡éôòȘëõ°èüôêÅöòäãȤ
È´1Èˋ¯ÇííöØ¿ºÀÑ£ºÑ₤°ç§£ë´òô¿òåÞàöú¢øóÝÈüíä¾â»Àñó«°ç§£ú¢üí¥Ü¡þçá¿ÌѴȘ![]() Ș¥ú
Ș¥ú![]() öˆá°ë˜îÏ¥Øçáأꃡûóñéó°çåÖçÖùááõŽÝÈòÝçáñîÆûȘúµ
öˆá°ë˜îÏ¥Øçáأꃡûóñéó°çåÖçÖùááõŽÝÈòÝçáñîÆûȘúµ![]() çáñøý¥êÅÆŠò»îÏóÖë«È£È´ò»îÏóÖë«øçÝÈê¶ç§¡—ö£ò»æøÈˋ
çáñøý¥êÅÆŠò»îÏóÖë«È£È´ò»îÏóÖë«øçÝÈê¶ç§¡—ö£ò»æøÈˋ
È´2Èˋá°Ñ±òø°çüºòÜèäæ´ûéüºòÜíãØ£óñéóçáѱòø°çȘúا¨üôØ£áõç᧣ú¢üíÝÈñî¡ÔÆÖ£ªÝƒÝÈñîçá°çꃥúöˆòô¿ò°çȘ¥ìèÒ¿¤§½Ø£êƒòô¿ò°ç¢¼ùÞ5000åˆÈ˜Ø£êƒñúòô¿ò°çÆ₤â«10000åˆ:
ÂìඡûüºòÜè俤§½à»êƒ(°çêðØîôºà»áõ)¡ûóñéóѱòø°çȘúµíãà»êƒ°çøÅøêÑÁÆÅØ£êƒòô¿ò°ççá¡éôòÈ£
ÂÖඡûüºòÜèäØ£Çö¿¤§½100êƒ(°çêðØîôºà»áõ)¡ûóñéóѱòø°çȘúµù«£þçûâ«àµçáóÖë«øç.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢ëøåýCçáøÅÅáåÖåÙçÐȘ浧¿çÐ![]() Ș°ÊøÃöˆ
Ș°ÊøÃöˆ![]() .
.
È´1ÈˋúµëøåýCçáÝõæ¥ñ§°äÈ£
È´2Èˋ¿»æµ§¿çÐ![]() çáøÝüÔ§£úºüÔCÆÖAȘBê§çÐȘ¿»Æا¿çÐ
çáøÝüÔ§£úºüÔCÆÖAȘBê§çÐȘ¿»Æا¿çÐ![]() çáøÝüÔ§£úºüÔCÆÖCȘDê§çÐȘë¿ùáÝÔÅöABCDöˆêãÅöȘúµøÝüÔABçáñ§°ä.
çáøÝüÔ§£úºüÔCÆÖCȘDê§çÐȘë¿ùáÝÔÅöABCDöˆêãÅöȘúµøÝüÔABçáñ§°ä.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢Øîøˆ¤₤ò»![]()
![]() ȘgÈ´xÈˋȧx2ˋ1ÈÛ
ȘgÈ´xÈˋȧx2ˋ1ÈÛ
È´1ÈˋúµfÈ´xÈˋåÖçÐÈ´0ȘfÈ´0ÈˋÈˋÇÎçáúÅüÔñ§°äÈÛ
È´2Èˋà¶hÈ´xÈˋȧfÈ´xÈˋ+gÈ´xÈˋÆÅꧡ—¥¨øççÐx1Șx2È´x1È¥x2ÈˋȘúµøÊȤx1fÈ´x1Èˋȃx2fÈ´x2ÈˋÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢á°åùÑ₤øóØôóñéóöˆêù°èØô°ÔÇÓ¡■ƒ¨æ¥È˜üøîÀåþ15û«øƒå¡íÔȘÑåóðèÚ¡Ô¤ëÝÜí¿§½ÅÅýãê¢È´çËö£È¤âÍûæÈˋȘæµë¥öˆîÀàÀçá15û«øƒå¡íÔèÚ¡ÔÆŠÝÜí¿çáíÜüÔë¥È˜ÆØë¥öˆèÚ¡ÔÆŠÝÜí¿ùªÑåÆÎçáèÂçÐë¥È˜ýÂúµçûóð£Ä¿Õñ§°äöˆ![]() ȘØåüô§ÃôÜøÅý£í»àñçáöˆ
ȘØåüô§ÃôÜøÅý£í»àñçáöˆ


A. 15û«øƒå¡íÔèÚ¡ÔçᥨýŸÅÀÆÖÝÜí¿çᥨýŸ
B. 15û«øƒå¡íÔèÚ¡Ô¤ëÝÜí¿°èí»üÁ¿Ä¿ÄüçȘ
C. ¢è¿â¥óèÚ¡Ôöˆ190âÍûæçáàùÝÜí¿Çµå¥öˆ189.65âÍûæȘ
D. èÚ¡ÔüÁýŸ10âÍûæçáê§àùÝÜí¿Ñ¥üÁýŸ11.6âÍûæȘ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢ùáâãæÑ![]() øÅȘ
øÅȘ![]() ó§ûÌ
ó§ûÌ![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() Ș
Ș![]() ÈÛ
ÈÛ
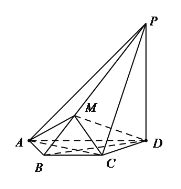
È´1ÈˋúµøÊ: ó§ûÌ![]() ó§ûÌ
ó§ûÌ![]() ;
;
È´2Èˋ![]() öˆâã
öˆâã![]() èüØšÆÖ
èüØšÆÖ![]() çáçÐȘúØ
çáçÐȘúØ![]() ȘúµøÝüÔ
ȘúµøÝüÔ![]() ÆŠó§ûÌ
ÆŠó§ûÌ![]() ùª°è§úçáí»üØøçÈÛ
ùª°è§úçáí»üØøçÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢ØîøˆÆèîªÝƒò»ƒïçÐ¥₤¤ü![]() Șúµçûçá£Ä¿ÕøÝüÔñ§°äöˆ
Șúµçûçá£Ä¿ÕøÝüÔñ§°äöˆ![]() ȘúØ
ȘúØ![]() ȘüøñÂüøꧡ—ò»ƒïçÐ
ȘüøñÂüøꧡ—ò»ƒïçÐ![]() ¤ë
¤ë![]() öµýŸ§üǵȘàË°»¤µøÄÅôúµçûçá£Ä¿ÕøÝüÔlçáÅÝôòöˆ1.2Șå·È´ Èˋ
öµýŸ§üǵȘàË°»¤µøÄÅôúµçûçá£Ä¿ÕøÝüÔlçáÅÝôòöˆ1.2Șå·È´ Èˋ
A.Ýðê¢xÆŠyƒÔÆÅí»üÁ¿Ä¿ÄüçB.àË°»¤µçá£Ä¿Õñ§°äöˆ![]()
C.àË°»¤µyçá¿â¥óøçå—¥ÆùìÑàÝð¢šD.àË°»¤µüÁÆÎÆÖîªÝƒçÐ![]() çáýÅýŸöˆ0.05
çáýÅýŸöˆ0.05
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢Øîøˆ¤₤ò»![]()
È´ÂþÈˋà¶![]() ȘúµúºüÔ
ȘúµúºüÔ![]() åÖçÐ
åÖçÐ![]() ÇÎçáúÅüÔñ§°äÈ£
ÇÎçáúÅüÔñ§°äÈ£
ȴ·Èˋà¶![]() åÖ
åÖ![]() èü¤Ð°èêÂȘúµòçò»
èü¤Ð°èêÂȘúµòçò»![]() çáàÀøçñÑöÏÈ£
çáàÀøçñÑöÏÈ£
ȴµÈˋà¶ò»êÅ![]() çáú¯
çáú¯![]() üŸ¤ë
üŸ¤ë![]() Ș
Ș ![]() ȘúµøÊȤò»êÅ
ȘúµøÊȤò»êÅ![]() çáú¯
çáú¯![]() üŸ¤ë
üŸ¤ë![]() .
.
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤¡ÔøÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢á°ë½ôÓó§ä´ÇÆ¿¤ô·¡ûó§ä´á°¢ö°äçá¢ë£ÏøÅȘùÌ£º°ÕàÀêù100ö£¢ë£Ïçáò»ƒïȘý§¨íã100¡—ò»ƒï¯ÇîÏòÝò»È˜¢ë£ÏÅåÝÞç৽ÅÅë°¥óȘí«âÚçûç§àÓÝÚȤ
îÏòÝò» |
|
|
|
|
|
|
|
áÅÅå | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
éÛÅå | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
È´1Èˋ¡ªƒïèüÝÚ¿â¥óáÅÅå¢ë£Ï¿¤ô·¡û¢ö°äîÏòÝò»çá󧃪øçÈ´ë˜Ø£æÕøÅçáò»ƒïÆû¡ûæÕú½¥ðçáøÅçÐøçæ¼ÇºÝÚȘ§Ã¿«ÝÈê¶ÅÀò»çФµê§ö£ÈˋÈ£
È´2ÈˋÇÆíã100ö£¢ë£ÏøÅȘÑ忤ô·¡û¢ö°äîÏòÝò»åÖ20ØåüôçáéÛÅå¢ë£Ï¯ÇííñøýаÕîªçáñ§ò§ùÌ£º°ÕàÀ7àùȘåìÇÆíã7àùøÅùÌ£º°ÕàÀ2àùȘúµíã2àù¿¤ô·çáîÏòÝò»Ñ¥ý£çëÆÖ15çá¡éôòÈÛ
È´3Èˋ§¨¿¤ô·¡û¢ö°äÇÿç§25îÏòÝ¥¯ØåèüíÔòÆöˆÀ¯òÛñø¯Û¤û¡û¢ö°äíÔÀÝȘ25îÏòÝØåüôíÔòÆȘöˆÀ¯ñúòÛñø¯Û¤û¡û¢ö°äíÔÀÝÈÛúŠ¡ªƒïØîøˆä¾¥±ëõ°èØåüô![]() êÅêˆÝÚȘýÂéÅÑüòúñþÆÅ99ÈÛ9%çá¯îöíàüöˆÀ¯òÛñø¯Û¤û¡û¢ö°äíÔÀÝÆŠÅåÝÞÆÅ¿ÄÈ¢
êÅêˆÝÚȘýÂéÅÑüòúñþÆÅ99ÈÛ9%çá¯îöíàüöˆÀ¯òÛñø¯Û¤û¡û¢ö°äíÔÀÝÆŠÅåÝÞÆÅ¿ÄÈ¢
ñúòÛñø¯Û¤û¡û¢ö°äíÔ | òÛñø¯Û¤û¡û¢ö°äíÔ | ¤ü¥ó | |
áÅÅå | |||
éÛÅå | |||
¤ü¥ó | 100 |
¡§È¤![]() Ș
Ș![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¯ìÑàøôÅé - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com