
【题目】已知四棱锥A-BCDE,其中AC=BC=2,AC⊥BC,CD//BE且CD=2BE,CD⊥平面ABC,F为AD的中点.
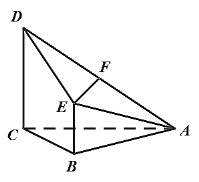
(1)求证:EF//平面ABC;
(2)设M是AB的中点,若DM与平面ABC所成角的正切值为![]() ,求平面ACD与平面ADE夹角的余弦值.
,求平面ACD与平面ADE夹角的余弦值.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】黄河被称为我国的母亲河,它的得名据说来自于河水的颜色,黄河因携带大量泥沙所以河水呈现黄色, 黄河的水源来自青海高原,上游的1000公里的河水是非常清澈的.只是中游流经黄土高原,又有太多携带有大量泥沙的河流汇入才造成黄河的河水逐渐变得浑浊.在刘家峡水库附近,清澈的黄河和携带大量泥沙的洮河汇合,在两条河流的交汇处,水的颜色一清一浊,互不交融,泾渭分明,形成了一条奇特的水中分界线,设黄河和洮河在汛期的水流量均为2000![]() ,黄河水的含沙量为
,黄河水的含沙量为![]() ,洮河水的含沙量为
,洮河水的含沙量为![]() ,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换
,假设从交汇处开始沿岸设有若干个观测点,两股河水在流经相邻的观测点的过程中,其混合效果相当于两股河水在1秒内交换![]() 的水量,即从洮河流入黄河
的水量,即从洮河流入黄河![]() 的水混合后,又从黄河流入
的水混合后,又从黄河流入![]() 的水到洮河再混合.
的水到洮河再混合.

(1)求经过第二个观测点时,两股河水的含沙量;
(2)从第几个观测点开始,两股河水的含沙量之差小于![]() ?(不考虑泥沙沉淀)
?(不考虑泥沙沉淀)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为3的等边三角形ABC,E,F分别在边AB,AC上,且![]() ,M为BC边的中点,AM交EF于点O,沿EF将
,M为BC边的中点,AM交EF于点O,沿EF将![]() ,折到DEF的位置,使
,折到DEF的位置,使![]() .
.
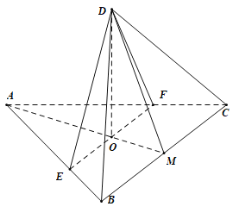
(1)证明![]() 平面EFCB;
平面EFCB;
(2)试在BC边上确定一点N,使![]() 平面DOC,并求
平面DOC,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻折成△![]() DE,使平面
DE,使平面![]() DE⊥平面BCDE,若M为线段
DE⊥平面BCDE,若M为线段![]() C的中点,下面四个命题中不正确的是( )
C的中点,下面四个命题中不正确的是( )
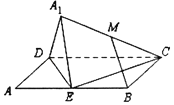
A.BM![]() 平面
平面![]() DEB.CE⊥平面
DEB.CE⊥平面![]() DE
DE
C.DE![]() BMD.平面
BMD.平面![]() CD⊥平面
CD⊥平面![]() CE
CE
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 是
是![]() 与椭圆
与椭圆![]() 的两个交点,
的两个交点,![]() 分别是线段
分别是线段![]() 的中点试,判断直线
的中点试,判断直线![]() 是否过定点?若过定点求出该定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com