
【题目】某葡萄基地的种植专家发现,葡萄每株的收获量![]() (单位:
(单位: ![]() )和与它“相近”葡萄的株数
)和与它“相近”葡萄的株数![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
| 1 | 2 | 3 | 5 | 6 | 7 |
| 15 | 13 | 12 | 10 | 9 | 7 |
(1)求该葡萄每株的收获量![]() 关于它“相近”葡萄的株数
关于它“相近”葡萄的株数![]() 的线性回归方程及
的线性回归方程及![]() 的方差
的方差![]() ;
;
(2)某葡萄专业种植户种植了1000株葡萄,每株“相近”的葡萄株数按2株计算,当年的葡萄价格按10元/ ![]() 投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
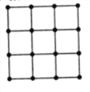
(3)该葡萄基地在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株葡萄,其中每个小正方形的面积都为![]() ,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
【答案】(1)线性回归方程为![]() ,方差为7;(2)总收入为
,方差为7;(2)总收入为![]() ;(3)见解析.
;(3)见解析.
【解析】【试题分析】(1)利用回归直线方程的公式,计算![]() 的值,由此求得回归直线方程.利用样本方差的公式计算得方差.(2)将
的值,由此求得回归直线方程.利用样本方差的公式计算得方差.(2)将![]() 代入回归直线方程,求得对应预报变量的值,进而求得总收入.(3)
代入回归直线方程,求得对应预报变量的值,进而求得总收入.(3)![]() 可能的取值为
可能的取值为![]() ,利用回归直线方程,求出对应
,利用回归直线方程,求出对应![]() 的值为
的值为![]() ,求得对应概率后列表得到分布列并计算出期望值.
,求得对应概率后列表得到分布列并计算出期望值.
【试题解析】
(1)由题意,可知![]() ,
,
![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以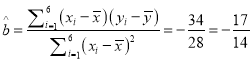 ,
,
所以![]() ,
,
故该葡萄每株收获量![]() 关于它“相近”葡萄的株数
关于它“相近”葡萄的株数![]() 的线性回归方程为
的线性回归方程为![]() .
.
![]() 的方差为
的方差为
![]()
![]() .
.
(2)由![]() ,可知当
,可知当![]() 时,
时, ![]() ,
,
因此总收入为![]() (万元).
(万元).
(3)由题知, ![]() .
.
由(1)(2),知当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() ,
,
即![]() 时,与之相对应的
时,与之相对应的![]() 的值分别为13,12,11,
的值分别为13,12,11,
又![]() ,
,
![]() ,
,
![]() ,
,
所以在所种葡萄中随机选取一株,它的收获量![]() 的分布列为
的分布列为
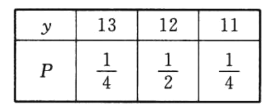
![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程:
的直角坐标方程:
(Ⅱ)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华民族是一个传统文化丰富多彩的民族,各民族有许多优良的传统习俗,如过大年吃饺子,元宵节吃汤圆,端午节吃粽子,中秋节吃月饼等等,让人们感受到浓浓的节目味道. 某小区有1200户家庭,全部居民在小区的8栋楼内,各家庭在过年时各自包有肉馅饺子、蛋馅饺子和素馅饺子三种味道的饺子(假设每个家庭包有且只包有这三种味道中的一种味道的饺子).
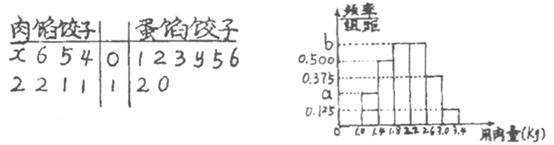
(1)现根据饺子的不同味道用分层抽样的方法从该小区随机抽样抽取![]() 户家庭,其中有10户家庭包的是素馅饺子,在抽取家庭中包肉馅饺子和蛋馅饺子的家庭分布在8栋楼内的住户数记录为如图所示的茎叶图,已知肉馅饺子数的中位数为10,蛋馅饺子数的平均数为5,求该小区包肉馅饺子的户数;
户家庭,其中有10户家庭包的是素馅饺子,在抽取家庭中包肉馅饺子和蛋馅饺子的家庭分布在8栋楼内的住户数记录为如图所示的茎叶图,已知肉馅饺子数的中位数为10,蛋馅饺子数的平均数为5,求该小区包肉馅饺子的户数;
(2)现从包肉馅饺子的家庭中随机抽取100个家庭调查包饺子的用肉量(单位: ![]() )得到了如图所示的频率分布直方图,若用肉量在第1小组
)得到了如图所示的频率分布直方图,若用肉量在第1小组![]() 内的户数为
内的户数为![]() (
(![]() 为茎叶图中的
为茎叶图中的![]() ),试估计该小区过年时各户用于包饺子的平均用肉量(各小组数据以组中值为代表).
),试估计该小区过年时各户用于包饺子的平均用肉量(各小组数据以组中值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,并根据图象:
轴左侧的图象,如图所示,并根据图象:

(1)直接写出函数![]() ,
, ![]() 的增区间;
的增区间;
(2)写出函数![]() ,
, ![]() 的解析式;
的解析式;
(3)若函数![]() ,
, ![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 。
。
(1)求实数a,b,并确定函数![]() 的解析式;
的解析式;
(2)判断![]() 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出![]() 的单调减区间,并判断
的单调减区间,并判断![]() 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)若抛物线![]() 的焦点到准线的距离为4,直线
的焦点到准线的距离为4,直线![]() ,求直线
,求直线![]() 截抛物线
截抛物线![]() 所得的弦长;
所得的弦长;
(2)过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,过点
两点,过点![]() 作抛物线的切线,两切线相交于点
作抛物线的切线,两切线相交于点![]() ,若
,若![]() 分别表示直线
分别表示直线![]() 与直线
与直线![]() 的斜率,且
的斜率,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,分别从两厂随机各选取了![]() 个轮胎,将每个轮胎的宽度(单位:
个轮胎,将每个轮胎的宽度(单位: ![]() )记录下来并绘制出如下的折线图:
)记录下来并绘制出如下的折线图:
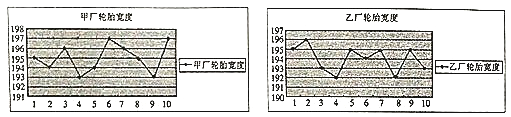
(1)分别计算甲、乙两厂提供的![]() 个轮胎宽度的平均值;
个轮胎宽度的平均值;
(2)轮胎的宽度在![]() 内,则称这个轮胎是标准轮胎.
内,则称这个轮胎是标准轮胎.
(i)若从甲乙提供的![]() 个轮胎中随机选取
个轮胎中随机选取![]() 个,求所选的轮胎是标准轮胎的概率
个,求所选的轮胎是标准轮胎的概率![]() ;
;
(ii)试比较甲、乙两厂分别提供的![]() 个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
个轮胎中所有标准轮胎宽度的方差大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个厂的轮胎相对更好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com