解:(Ⅰ)f(x)在[-1,1]上为增函数
证明:设x
1,x
2∈[-1,1],且x
1<x
2,在
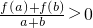
中,令a=x
1,b=-x
2,有
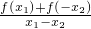
>0,
∵x
1<x
2,∴x
1-x
2<0,又∵f(x)是奇函数,
∴f(-x
2)=-f(x
2),∴

>0
∴f(x
1)-f(x
2)<0,即f(x
1)<f(x
2).
故f(x)在[-1,1]上为增函数…(6分)
(Ⅱ)∵f(1)=1 且f(x )在[-1,1]上为增函数,对x∈[-1,1],有f(x)≤f(1)=1.
由题意,对所有的x∈[-1,1],b∈[-1,1],有f(x)≤m
2-2bm+1恒成立,
应有m
2-2bm+1≥1?m
2-2bm≥0. 记g(b)=-2mb+m
2,对所有的b∈[-1,1],g(b)≥0成立.
只需g(b)在[-1,1]上的最小值不小于零…(8分)
若m>0时,g(b)=-2mb+m
2是减函数,故在[-1,1]上,b=1时有最小值,
且[g(b)]
最小值=g(1)=-2m+m
2≥0?m≥2;
若m=0时,g(b)=0,这时[g(b)]
最小值=0满足题设,故m=0适合题意;
若m<0时,g(b)=-2mb+m
2是增函数,故在[-1,1]上,b=-1时有最小值,
且[g(b)]
最小值=g(-1)=2m+m
2≥0?m≤-2.
综上可知,符合条件的m的取值范围是:m∈(-∞,-2]∪{0}∪[2,+∞).
分析:(Ⅰ)f(x)在[-1,1]上为增函数,利用函数的单调性定义,结合a+b≠0时,有
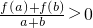
成立,可证;
(Ⅱ) 根据f(x)在[-1,1]上为增函数,对所有的x∈[-1,1],b∈[-1,1],有f(x)≤m
2-2bm+1恒成立,应有m
2-2bm+1≥f(1)=1?m
2-2bm≥0. 记g(b)=-2mb+m
2,对所有的b∈[-1,1],g(b)≥0成立,从而只需g(b)在[-1,1]上的最小值不小于零,故可解.
点评:本题的考点是函数恒成立问题,以奇函数为依托,证明函数的单调性,考查函数恒成立问题,关键是转换为研究函数的最值.

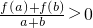 成立.
成立.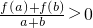 中,令a=x1,b=-x2,有
中,令a=x1,b=-x2,有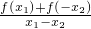 >0,
>0, >0
>0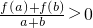 成立,可证;
成立,可证;
